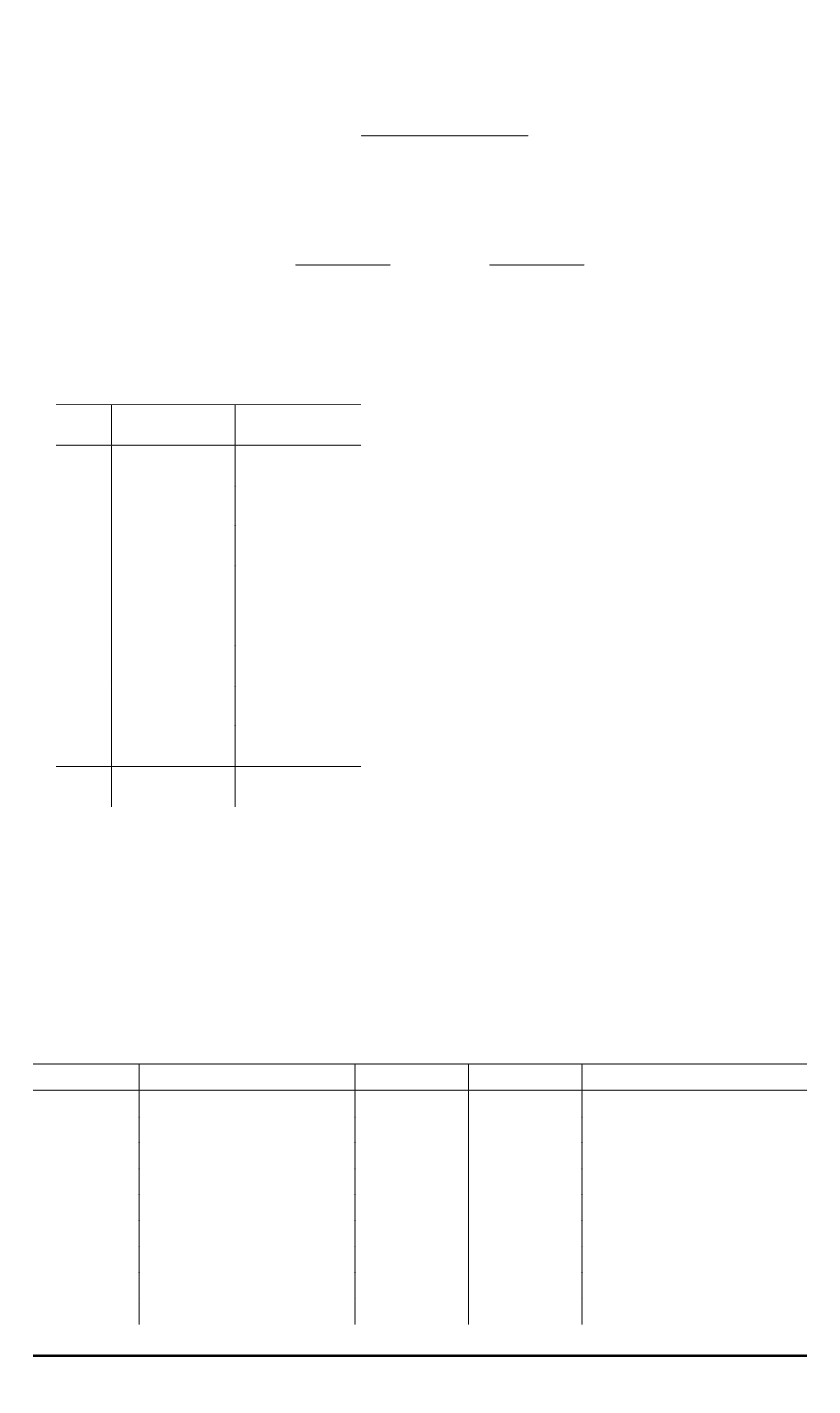
В этом случае поправочный коэффициент к базовой страховой пре-
мии вычисляется по формуле
k
s
=
(
b
−
1)(
a
+
k
ˉ
x
)
a
(
b
−
1 +
k
)
.
Оценки параметров для гамма-экспоненциальной модели имеют
вид
ˆ
a
=
μ
1
μ
2
μ
2
−
2
μ
2
1
,
ˆ
b
= 2
μ
2
−
μ
2
1
μ
2
−
2
μ
2
1
.
Таблица 1
Данные о страховых выплатах
по Италии
k
fk
nk
0
0,8631
863100
1 0,111161 111161
2 0,020405
20405
3 0,00403
4030
4 0,000929
929
5 0,000246
246
6 0,000129
129
7
0
0
Всего
1000000
Численный расчет страховых
премий
. Следует заметить, что ре-
альные данные о числе страховых
случаев, а тем более о страховых
выплатах по ним найти весьма труд-
но. Более или менее подробные дан-
ные относительно Бельгии содер-
жатся в работе [1]. Мы рассмотрим
наши модели на примере реальных
данных по Италии [7]. В данной ра-
боте приведена частота числа стра-
ховых случаев без указания обще-
го числа. Мы возьмем общее чи-
сло страховых случаев за 1 000 000.
Данные по Италии приведены
в табл. 1.
В следующих табл. 2–4 приведены оптимальные СБМ, построен-
ные с использованием различных моделей описания числа страховых
случаев. В этих системах бонус-малус учитывается только количество
страховых случаев. Премии рассчитаны в процентах по отношению к
базовой премии.
Таблица 2
Гамма-пуассоновская модель:
α
= 0
,
5138
,
λ
= 3
,
0263
,
p
= 0
,
7516
m
\
k
0
1
2
3
4
5
0
100
1
75,2
221,5
367,7
514,0
660,3
806,6
2
60,2
177,4
294,6
411,8
528,9
646,1
3
50,2
148,0
245,7
343,4
441,2
538,9
4
43,1
126,9
210,7
294,6
378,4
462,2
5
37,7
111,1
184,5
257,9
331,2
404,6
6
33,5
98,8
164,0
229,3
294,5
359,8
7
30,2
88,9
147,7
206,4
265,2
323,9
8
27,4
80,9
134,3
187,7
241,1
294,5
88
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 4


