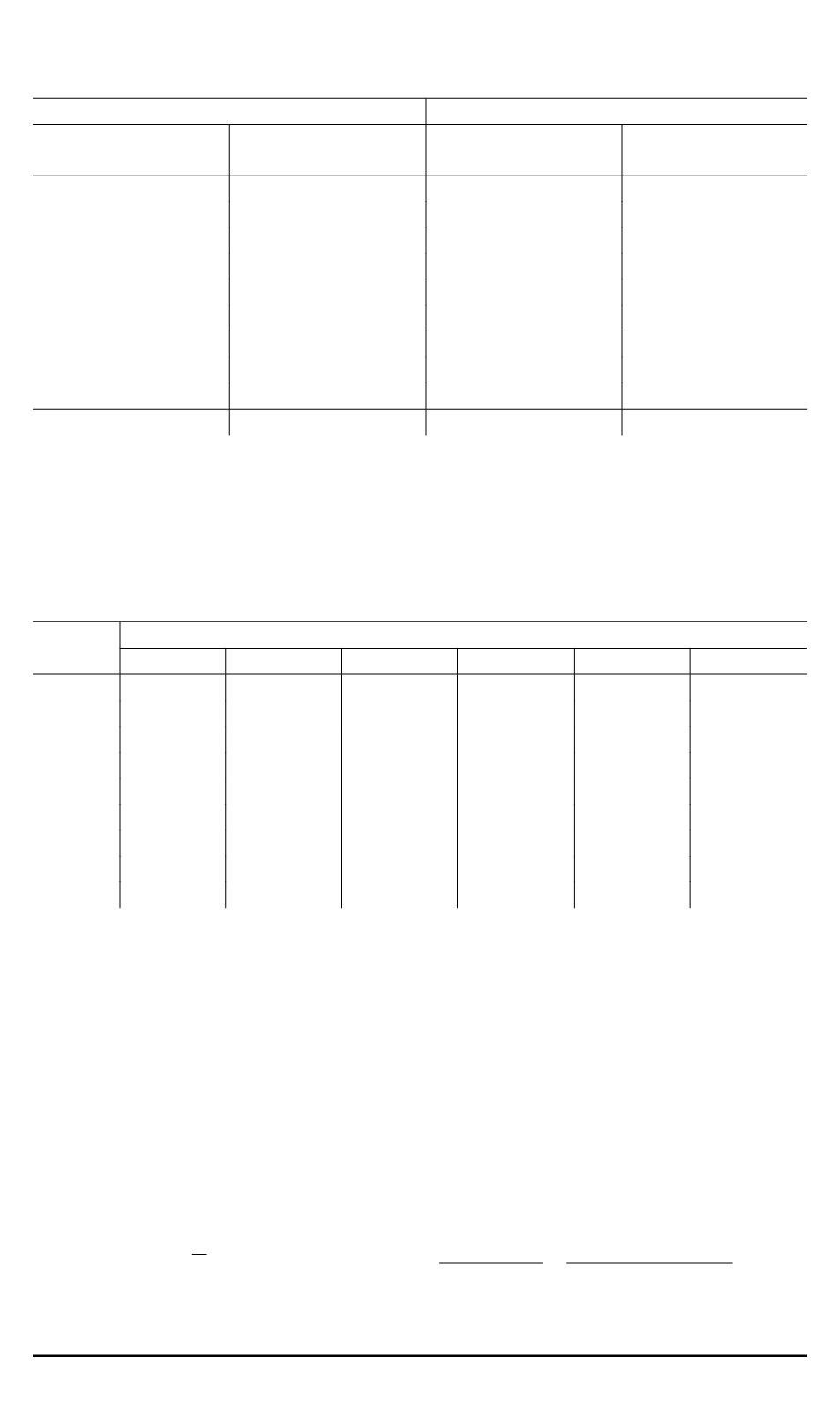
Таблица 5
Страховые данные по Бельгии
По количеству страховых случаев
По стоимости страховых случаев
Число страховых
случаев
Количество
страховых случаев
Число страховых
случаев
Средняя стоимость
0
96978
34368
466
1
9420
29408
1462
2
704
27432
2443
3
43
36473
3874
4
9
44059
6935
5
0
28409
13884
6
0
16435
29886
7
0
4440
66675
4306
499755
Всего
106974
225330
17336,6
В табл. 6 приведена оптимальная СБМ, построенная с использова-
нием гамма-пуассоновской модели и учитывающая только число стра-
ховых случаев.
Таблица 6
Гамма-пуассоновская модель:
α
= 1
,
605
,
λ
= 15
,
878
,
p
= 0
,
941
k
m
0
1
2
3
4
5
0
100
1
94,1
152,7
211,3
269,9
328,5
387,2
2
88,8
144,2
199,5
254,8
310,2
365,5
3
84,1
136,5
188,9
241,3
293,7
346,1
4
79,9
129,6
179,4
229,2
279,0
328,7
5
76,1
123,4
170,8
218,2
265,6
313,0
6
72,6
117,8
163,0
208,2
253,5
298,7
7
69,4
112,6
155,9
199,1
242,4
285,6
8
66,5
107,9
149,4
190,8
232,2
273,7
Из табл. 6 видно, что одна и та же модель оптимальной СБМ для
различных стран дает размеры страховых премий, существенно отли-
чающиеся друг от друга. Так, страхователь, имевший в течение пер-
вого года один страховой случай в Италии, в следующем году должен
платить страховую премию в размере 221,5% от базовой, в то время
как в Бельгии эта премия составляет 152,7%.
Для расчета страховых премий с учетом не только числа страхо-
вых случаев, но и размера страховых выплат по ним, воспользуемся
следующей формулой:
P
0
(
m, k, x
) =
k
s
P
0
(
m, k
) = 100
(
α
+
k
)
λ
α
(
λ
+
m
)
∙
(
b
−
1)(
a
+
k
ˉ
x
)
a
(
b
−
1 +
k
)
,
где
α
= 1
,
605
,
λ
= 15
,
878
,
a
= 19725
,
98
,
b
= 2
,
138
.
90
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 4


