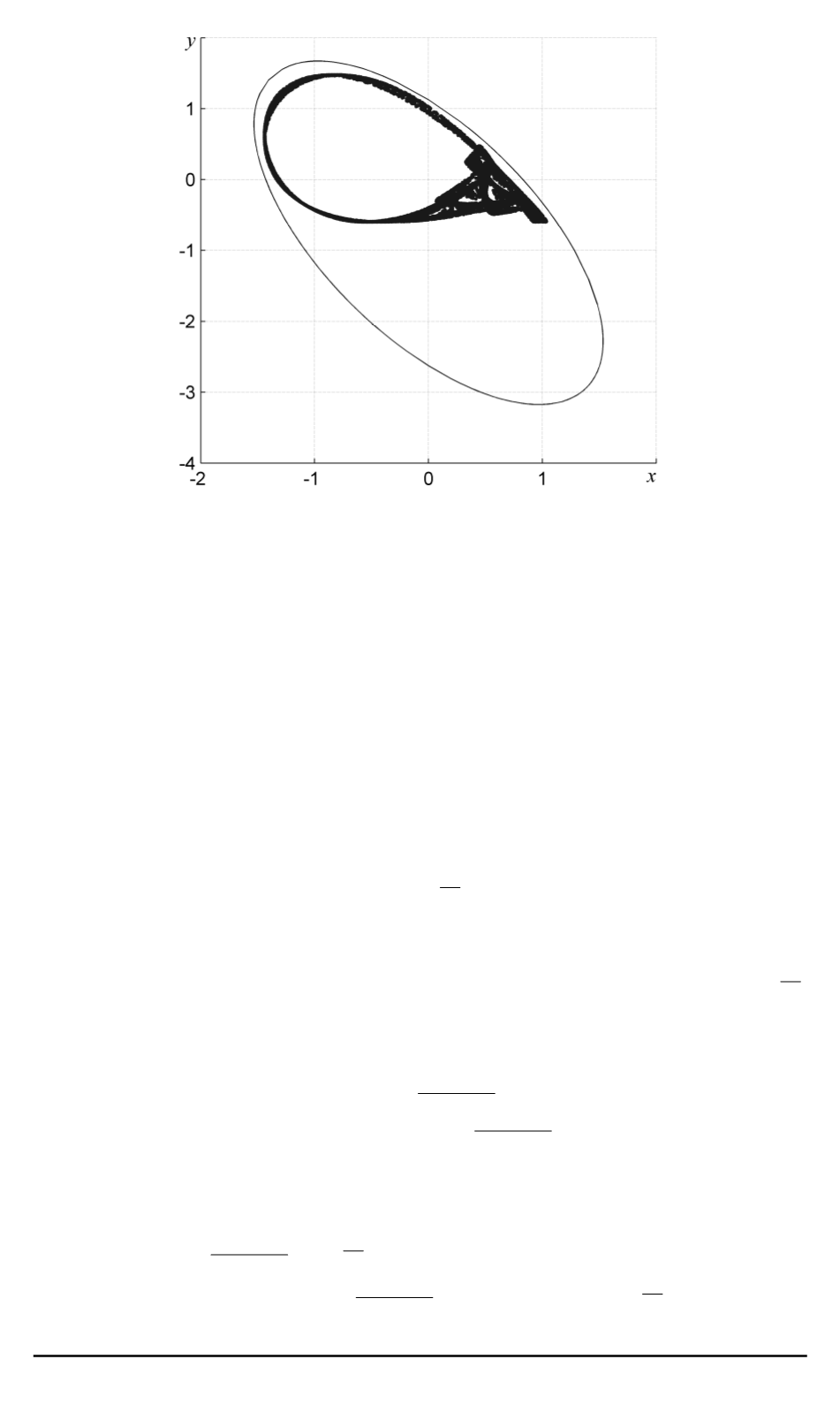
Рис. 4. Аттрактор системы Катала и граница локализирующего множе-
ства
F
−
2
(Ω
l
)
локализирующее множество совпадает с плоскостью. Анализ парабо-
лической функции более сложен технически, но приводит к тому же
результату: локализирующее множество совпадает с плоскостью.
Возможны две причины тривиального результата: неудачный вы-
бор локализирующих функций и обширность объединения отрица-
тельно инвариантных компактов, близкого ко всей плоскости. Оказы-
вается, что для системы Катала имеет место как раз вторая причина:
каждая точка плоскости принадлежит отрицательно инвариантному
компакту.
Теорема 5.
Существует такое
C
0
>
0
,
что для любого
C
≥
C
0
прямоугольник
P
C
=
{
(
x, y
) :
|
x
| ≤ √
C,
|
y
−
p
2
| ≤
C
}
является отри-
цательно инвариантным множеством системы Катала
(3)
.
Доказательство.
Для некоторой постоянной
C >
0
рассмо-
трим прямоугольник
P
C
и точку
(
x
0
, y
0
)
2
P
C
. Тогда
|
x
0
| ≤ √
C
,
|
y
0
−
p
2
| ≤
C
. Точка
(
x
0
, y
0
)
может иметь два прообраза, любой из
которых обозначим
(
x
−
1
, y
−
1
)
. Из уравнений (3) находим
(
x
−
1
=
± √
y
0
−
p
2
,
y
−
1
=
x
0
p
1
√
y
0
−
p
2
.
Если
y
0
< p
2
, то точка
(
x
0
, y
0
)
не имеет прообразов. Рассмотрим
случай
y
≥
p
2
. Тогда
|
x
−
1
|
=
√
y
0
−
p
2
≤
√
C,
|
y
−
1
−
p
2
| ≤ |
x
0
|
+
p
1
√
y
0
−
p
2
+
|
p
2
| ≤
(1 +
p
1
)
√
C
+
|
p
2
|
.
16
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 1


