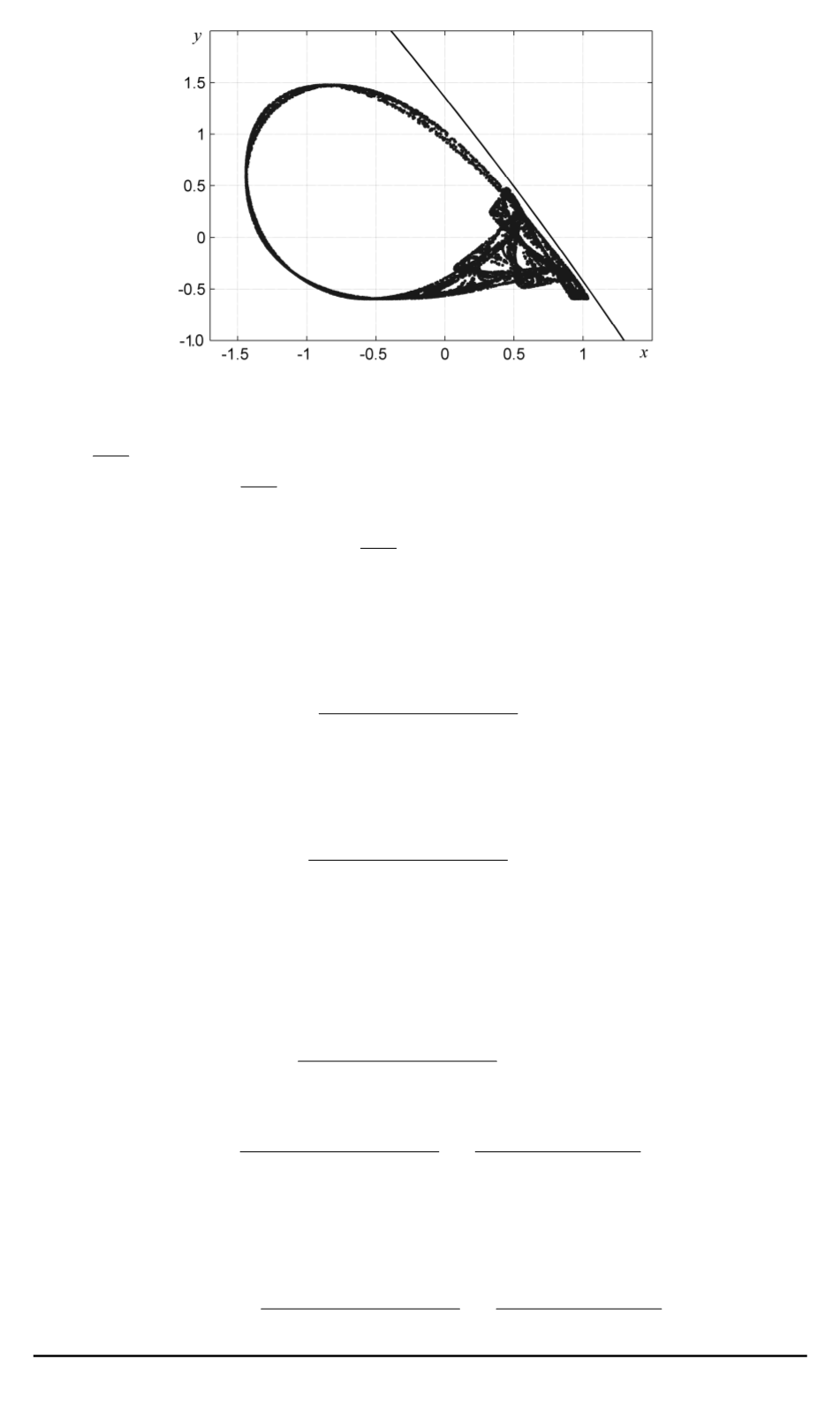
Рис. 2. Аттрактор системы Катала и граница локализирующего множества
Если множество
G
описывается системой неравенств
h
i
(
x
)
≤
0
,
i
= 1
, s
, то множество
F
−
1
(
G
)
описывается системой неравенств
h
i
(
F
(
x
))
≤
0
,
i
= 1
, s
. Действительно, условие
x
2
F
−
1
(
G
)
по опре-
делению означает, что
F
(
x
)
2
G
, а это условие эквивалентно системе
неравенств
h
i
(
F
(
x
))
≤
0
,
i
= 1
, s
.
Рассмотрим локализирующее множество
Ω
l
, определяемое нера-
венством (9). Как вытекает из приведенных рассуждений, множество
F
−
1
(Ω
l
)
описывается неравенством
p
2
+
x
2
≤
min
A>
1
A
2
(
A
−
p
1
)
2
−
4
p
2
4(
A
−
1)
−
A
(
p
1
x
+
y
)
.
Такое представление не очень удобно. Будем рассуждать несколько
иначе. Множество
Ω
lA
,
A >
1
, описываемое неравенством
y
≤
A
2
(
A
−
p
1
)
2
−
4
p
2
4(
A
−
1)
−
Ax,
является локализирующим для положительно инвариантных компак-
тов (оно получено с помощью локализирующей функции
ϕ
A
(
x, y
) =
=
Ax
+
y
). Его прообраз
F
−
1
(
G
lA
)
, также являющийся локализирую-
щим, описывается неравенством
p
2
+
x
2
≤
A
2
(
A
−
p
1
)
2
−
4
p
2
4(
A
−
1)
−
A
(
p
1
x
+
y
)
,
или
y
≤
A
2
(
A
−
p
1
)
2
−
4
p
2
4
A
(
A
−
1)
−
x
2
+
p
1
Ax
+
p
2
A
.
Пересечение
T
A>
1
F
−
1
(Ω
lA
)
найденных локализирующих множеств
описывается неравенством
y
≤
min
A>
1
A
2
(
A
−
p
1
)
2
−
4
p
2
4
A
(
A
−
1)
−
x
2
+
p
1
Ax
+
p
2
A
.
14
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 1


