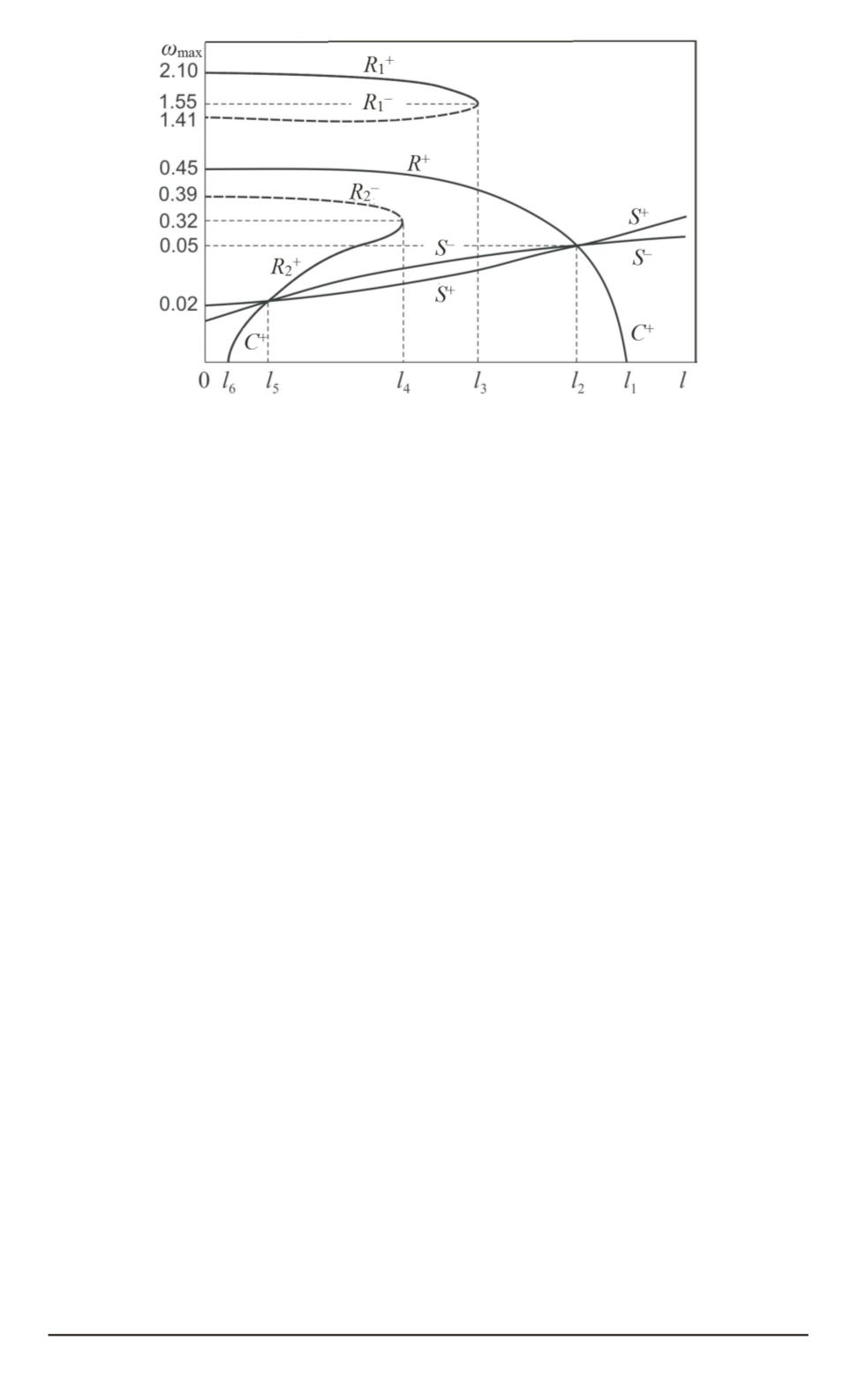
Рис. 10. Зависимости максимальных по углу
ϑ
значений угловой скорости
ω
max
на характерных фазовых траекториях от длины державки
Прокомментируем этот рисунок. При
l > l
1
=
e
m
выходящая из
седловой точки
M
3
(
−
π,
0)
сепаратриса
S
−
расположена ниже входя-
щей в седловую точку
M
2
(
π,
0)
сепаратрисы
S
+
. Все остальные фазо-
вые траектории стягиваются в начало координат — точку
M
1
(0
,
0)
—
единственный аттрактор, которому соответствует устойчивое положе-
ние равновесия маятника “по потоку”. Первое критическое значение
длины державки
l
=
l
1
=
e
m
. В этом случае точка
M
1
(0
,
0)
с точ-
ностью до членов третьего порядка малости является центром. Как
только длина державки станет меньше первого критического значения,
характер фазового портрета качественно меняется. Точка
M
1
(0
,
0)
ста-
новится седловой и порождает пару неустойчивых фокусов
M
4
(
α
r
,
0)
и
M
5
(
−
α
r
,
0)
. Таким образом, все три точки неустойчивы, также не-
устойчивы и седловые точки
M
2
(
π,
0)
,
M
3
(
−
π,
0)
. В силу диссипатив-
ности системы в целом, сепаратрисы, выходящие из точки
M
1
(0
,
0)
,
не могут уйти в бесконечность, вследствие чего возникают замкнутые
траектории. Сначала это одна замкнутая траектория
С
+
, охватыва-
ющая три точки
M
1
(0
,
0)
,
M
4
(
α
r
,
0)
,
M
5
(
−
α
r
,
0)
. Такой цикл как бы
наследует свойства единственного аттрактора, который имел место
при
l > e
m
. Эта особая бифуркация Андронова – Хопфа обусловлена
наличием динамической симметрии в рассматриваемой системе и ха-
рактером нелинейности позиционной силы. Траектория
С
+
является
единственным аттрактором.
При дальнейшем уменьшении значения
l
цикл
С
+
расширяется, се-
паратрисы
S
−
и
S
+
опускаются, и при некотором новом критическом
значении длины державки
l
=
l
2
< l
1
(
l
2
= 0
,
4245
) две сепаратрисы
совпадают, образуя петлю сепаратрис. На эту же петлю накладывается
и расширившийся до предела цикл
С
+
. Раскручивающимся фазовым
траекториям, лежащим внутри указанной петли, соответствуют все
более размашистые колебания маятника, не совершающего ни одного
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2014. № 2
45


