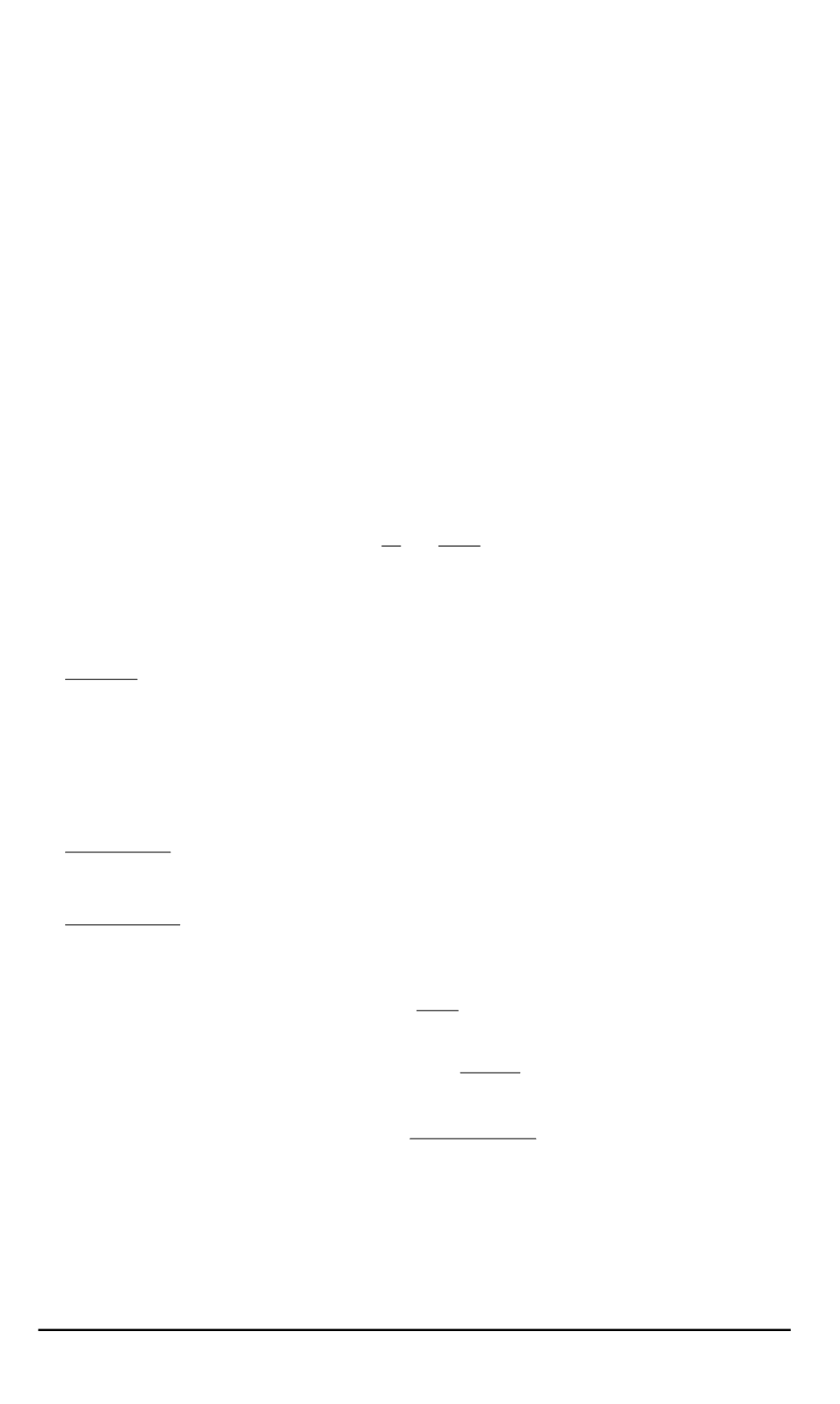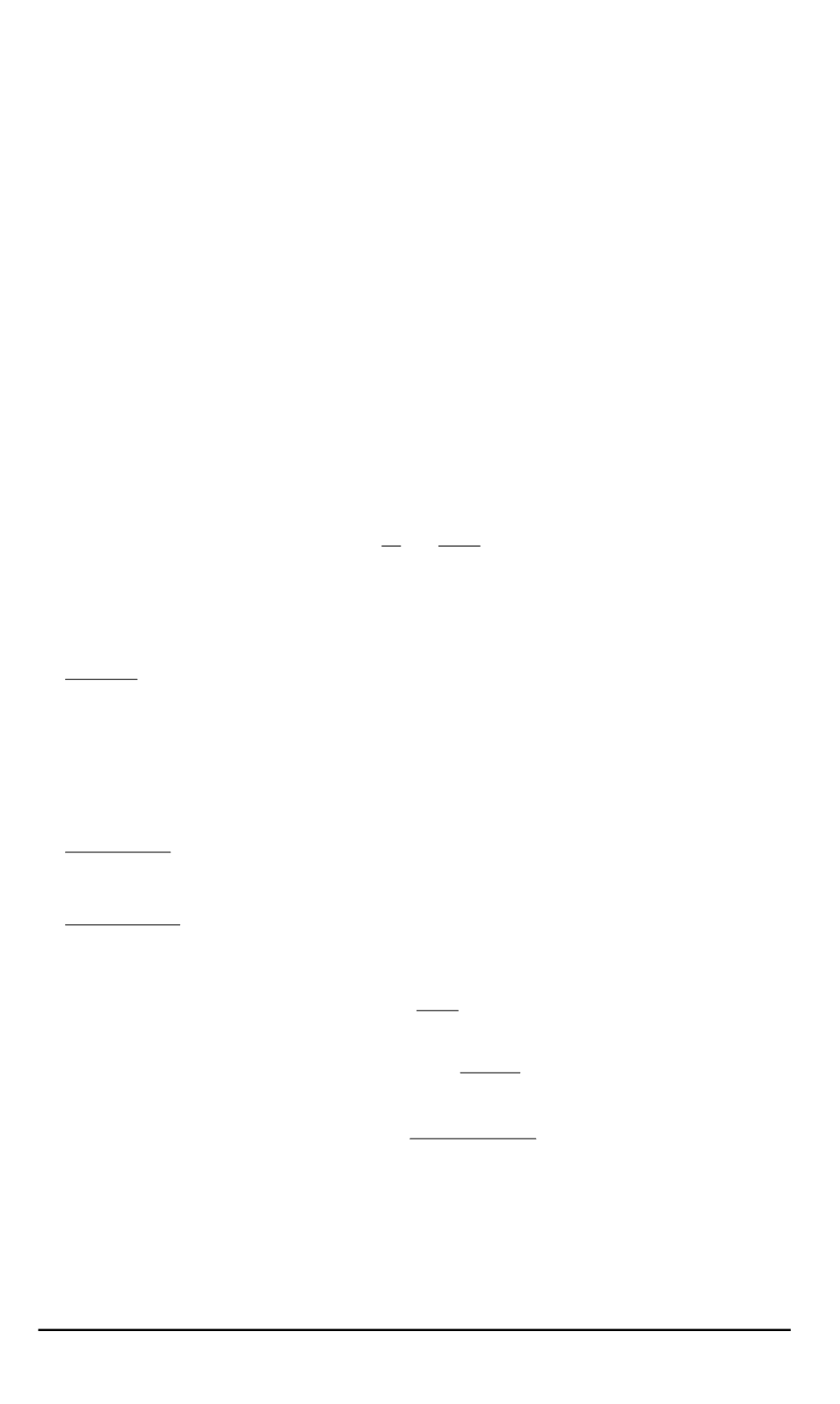
заданными функциями температуры
;
h
—
толщина окна
;
λ
к
—
ко
-
эффициент теплопроводности при комнатной температуре
T
к
;
σ
0
—
постоянная Больцмана
;
α
—
коэффициент теплообмена между поверх
-
ностью диэлектрического окна и газом со стороны невакуумной части
волновода
.
Известно
[8],
что решение нелинейной краевой задачи
(1) – (4)
при
заданных начальных
(2)
и граничных
(3), (4)
условиях является един
-
ственным в классе функций
,
непрерывных вместе с первыми и вторы
-
ми частными производными при условии
,
что функции
C
(Θ)
,
λ
(Θ)
и
Q
(
x, y, τ,
Θ)
являются гладкими
.
Поскольку в работе предполагается
,
что температурное поле
Θ(
x, y, τ
)
диэлектрического окна соответствует импульсному режиму
прибора СВЧ
,
то краевая задача
(1) – (4)
является сингулярно возму
-
щенной краевой задачей
[9, 10].
Действительно
,
вводя в рассмотрение безразмерное время
τ
0
по
формуле
τ
0
=
t
t
и
=
H
2
a
2
к
t
и
τ,
(5)
где
t
и
—
продолжительность импульса
(
далее вместо
τ
0
пишем
τ
),
име
-
ем
∂
(
C
Θ)
∂τ
=
ε
в
div
[
λ
grad Θ]
−
M
2
в
(Θ
−
Θ
к
)
−
σ
в
ˉ
ε
Θ
4
+
ε
в
Q,
(6)
a
0
< x < b, c < y < d,
0
< τ <
1
, a
0
<
0
, c <
0
, b >
0
, d >
0
,
Θ(
x, y, τ
)
|
τ
=0
= Θ
0
(
x, y
)
, a
0
≤
x
≤
b, c
≤
y
≤
d,
(7)
Θ(
x, y, τ
)
|
x
=0
, y
=0
<
∞
,
0
≤
τ
≤
1
,
(8)
∂
Θ(
x, y, τ
∂x
x
=
a
0
, x
=
b
= 0
, c
≤
y
≤
d,
0
≤
τ
≤
1
,
(9)
∂
Θ(
x, y, τ
)
∂y
y
=
c, y
=
d
= 0
, a
0
≤
x
≤
b,
0
≤
τ
≤
1;
(10)
здесь
ε
в
=
a
2
к
t
и
H
2
,
(11)
M
2
в
=
ε
в
M
2
=
a
2
к
t
и
α
λ
к
hH
,
(12)
σ
в
=
ε
в
σ
=
a
2
к
t
и
2
σ
0
T
3
макс
λ
к
h
.
(13)
Поскольку рассматривается импульсный режим работы приборов
СВЧ
,
то
t
и
1
с и
,
значит
,
безразмерный параметр
ε
в
(
в предположе
-
нии
,
что
(
a
2
к
/H
2
) =
O
(1)
)
удовлетворяет неравенству
ε
в
1
.
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
2
109