и краевыми условиями
B
0
1
B
0
2
¯ ¯ ¯
u
0
=0
=
−
(
τ
0
+
n
)
,
B
0
1
¯ ¯ ¯
u
0
=1
= 0
,
B
0
1
¯ ¯ ¯
τ
0
=0
=
ω
0
0
.
(50)
Для нахождения решения
ω
0
0
задачи
(47)–(48)
строилась система
,
ана
-
логичная системе
(42).
Асимптотическое решение задачи
(38)–(39)
по переменным
(˜
τ ,
˜
u
)
связано с асимптотическим решением задачи
(45)–(48)
по переменным
(
τ
0
, u
0
)
следующим образом
:
˜
ω
=
∂
2
f
∂η
2
= 0
,
5(
τ
0
)
−
1
/
2
∂
2
ϕ
∂ζ
2
= 0
,
5(
τ
0
)
−
1
/
2
ω
0
,
τ
0
=
1
˜
τ
,
u
0
= 0
,
5 ˜
τ
1
/
2
˜
u,
˜
ω
(˜
u,
˜
τ
) = 0
,
5(
τ
0
)
−
1
/
2
ω
0
(
u
0
, τ
0
)
,
˜
ω
(˜
u,
˜
τ
) = 0
,
5
√
˜
τ ω
0
µ
0
,
5
√
˜
τ
˜
u,
1
˜
τ
¶
.
Двумерная нестационарная задача формирования пограничного
слоя
(36)–(37)
решена для области
ξ
∈
[0
,
∞
]
.
Задача
(36)–(37)
рассмотрена для случаев
n
= 0
и
n
= 1
.
Пер
-
вому отвечает ситуация
,
когда жидкость в пограничном слое достига
-
ет скорости внешнего течения
U
=
u
0
x
очень быстро
,
т
.
е
.
приводит
-
ся в движение рывком
.
Тогда пограничный слой также стабилизиру
-
ется быстро
,
и функция
˜
ω
(˜
τ ,
˜
u
)
переходит в
ω
0
(
u
)
.
При
n
= 1
проис
-
ходит разгон жидкости с ускорением
. C
ечения полученных решений
˜
ω
(˜
τ ,
˜
u
)
и
ω
0
(
τ
0
, u
0
)
по переменным
˜
τ
= ˜
τ
k
и
τ
0
=
τ
0
k
соответственно
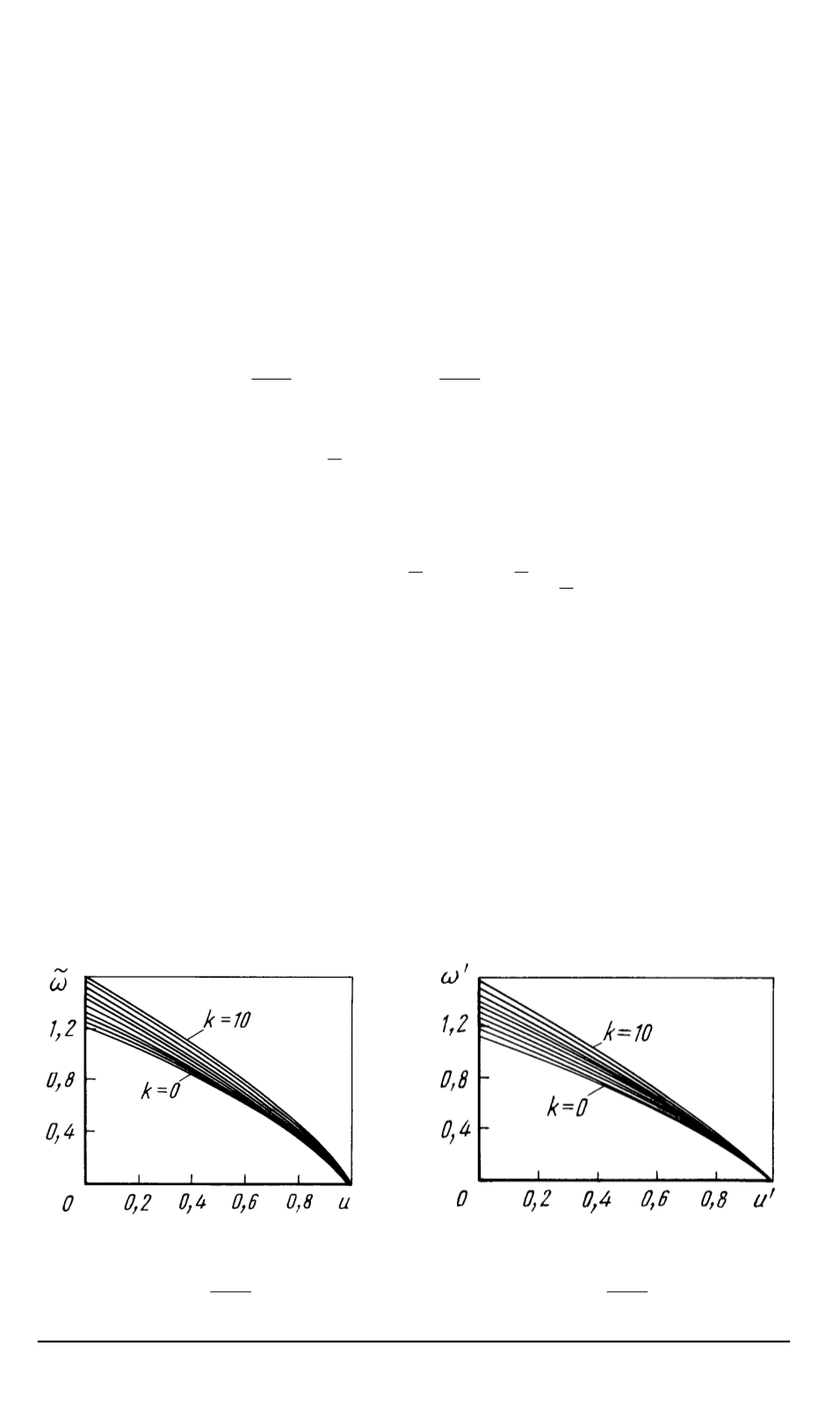
Рис
. 4.
Случай
n
= 1
.
Изменение
˜
ω
(˜
τ ,
˜
u
)
поперек пограничного слоя
при
˜
τ
= 0
,
1
k
,
k
= 0
,
10
Рис
. 5.
Случай
n
= 1
.
Изменение
ω
0
(
τ
0
, u
0
)
поперек пограничного слоя
при
τ
0
= 0
,
1
k
,
k
= 0
,
10
ISSN 0236-3933.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2004.
№
1 69


