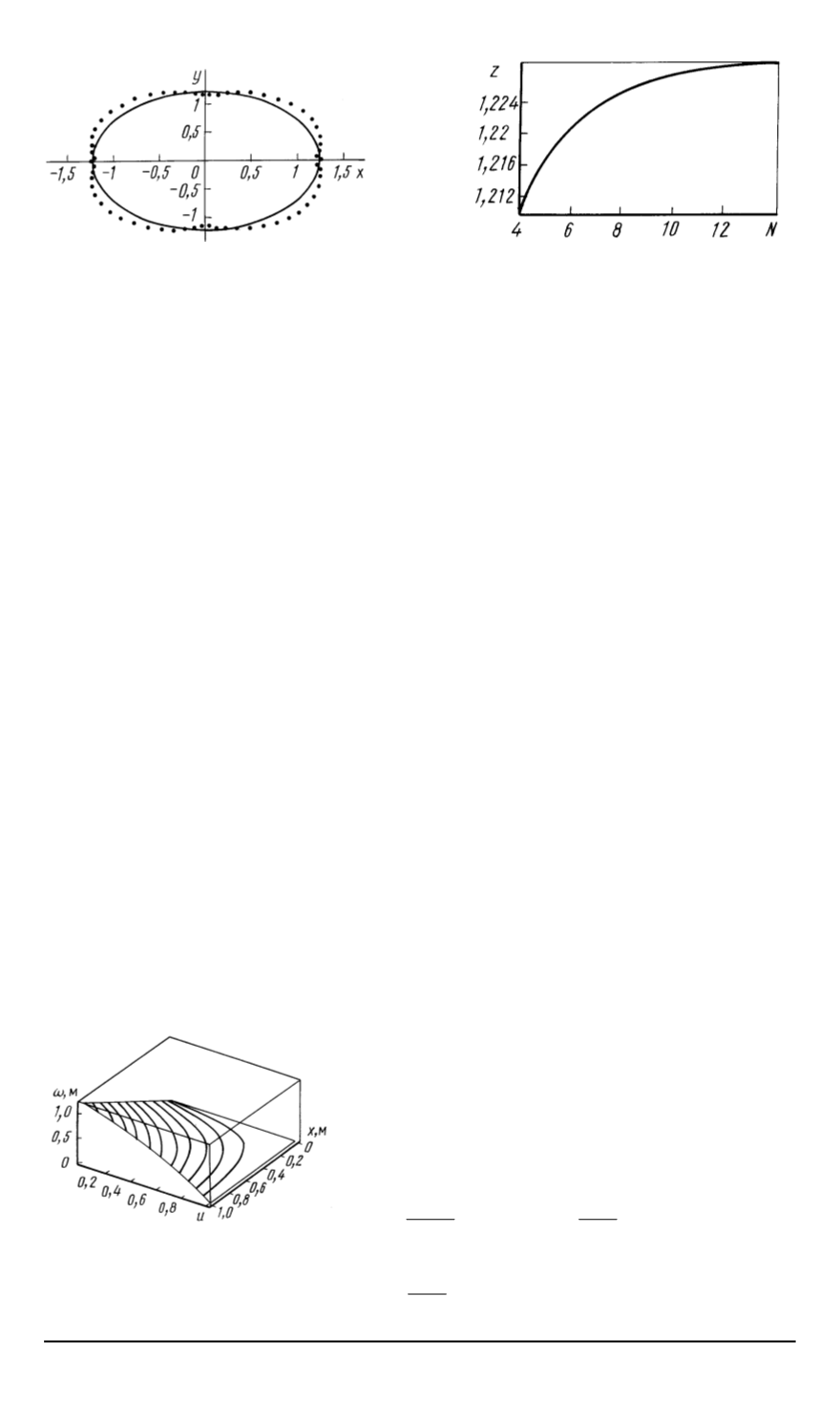
Рис
. 1.
Спектр корней
,
реализуе
-
мый из условия связи с внешним
потоком
Рис
. 2.
Зависимость значений
действительного положительного
корня от порядка приближения
N
найти корни первого уравнения системы
(29).
Среди корней показан
-
ных на рис
. 1,
при любом приближении существует один действитель
-
ный положительный корень
,
который будем использовать при постро
-
ении решения
.
Зависимость значений этого корня от числа учтенных
слагаемых уравнения представлена на рис
. 2.
При выбранном прибли
-
жении
(
N
= 10
)
корню
z
= 1
,
2276
соответствует решение
ω
(
x, u
) = 1
,
2276
x
−
0
,
8146
xu
−
0
,
2703
xu
2
−
0
,
0436
xu
3
−
−
0
,
0362
xu
4
−
0
,
0187
xu
5
−
. . .
=
xω
0
(
u
)
,
(30)
представленное на рис
. 3.
Полученное решение имеет вид
ω
=
xω
0
(
u
)
(31)
и задает распределение функции
ω
по координате
x
.
Подстановка ре
-
шения
(30)
в уравнение
(17)
приводит к оценке
∆
ω
= 0
,
1
·
10
−
1
x
3
+ 0
,
5
·
10
−
9
x
3
u
−
0
,
3
·
10
−
9
x
3
u
2
+ 0
,
4
·
10
−
9
x
3
u
3
+
. . . ,
условие на внешней границе выполняется с точностью до
∆(
ω
|
u
=1
) =
−
0
,
845
·
10
−
9
x.
Рис
. 3.
Решение стационарной
задачи
Предложенный метод позволил дока
-
зать вид решения
(31),
который в рабо
-
те
[4]
задается для скоростей из дополни
-
тельных соображений
.
Подставив реше
-
ние
(31)
в уравнение
(17),
придем к зада
-
че
ω
2
0
d
2
ω
0
du
2
+ (
u
2
−
1)
dω
0
du
−
uω
0
= 0
,
(32)
ω
0
dω
0
du
¯ ¯ ¯ ¯
u
=0
=
−
1
,
ω
0
|
u
=1
= 0
,
(33)
64 ISSN 0236-3933.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2004.
№
1


