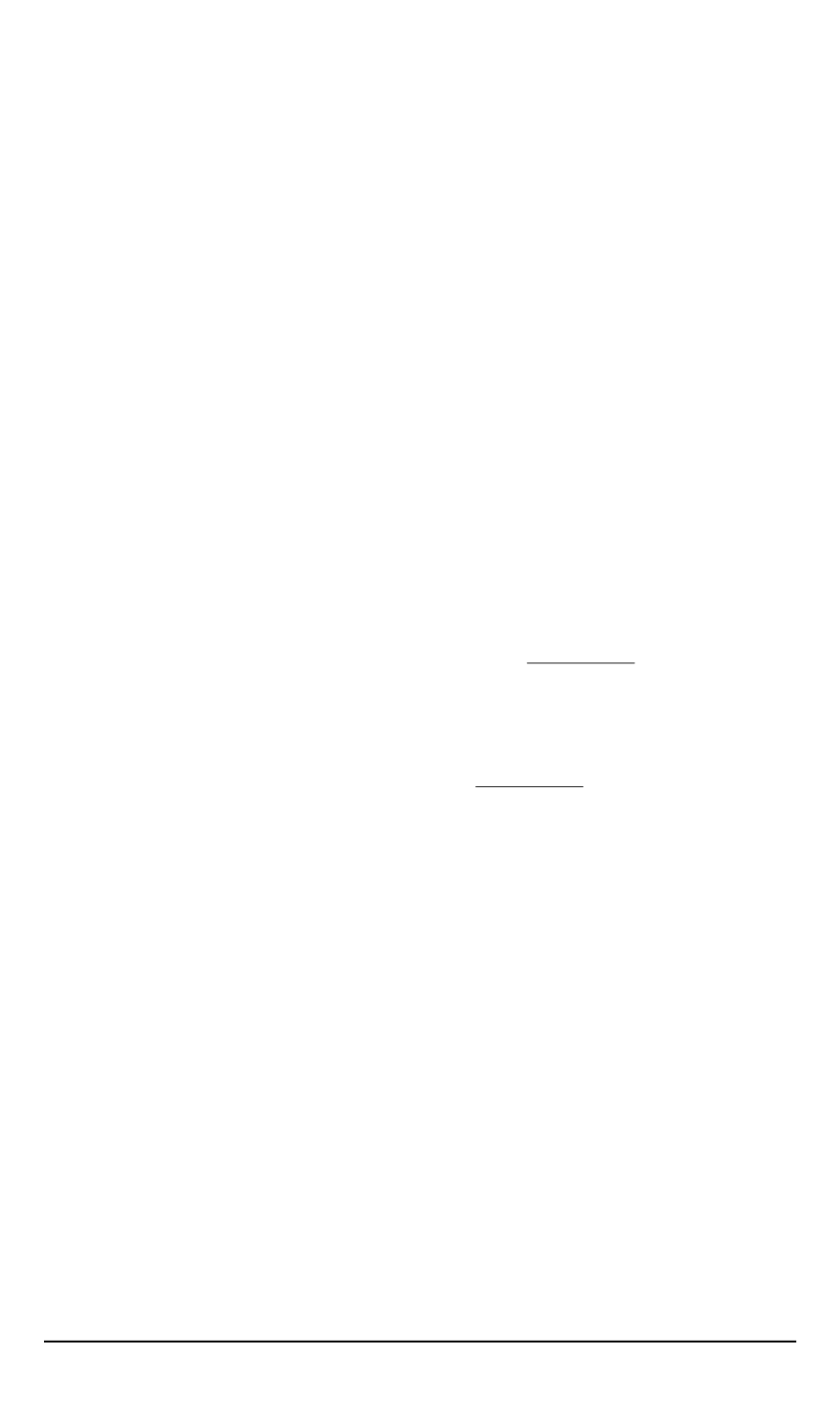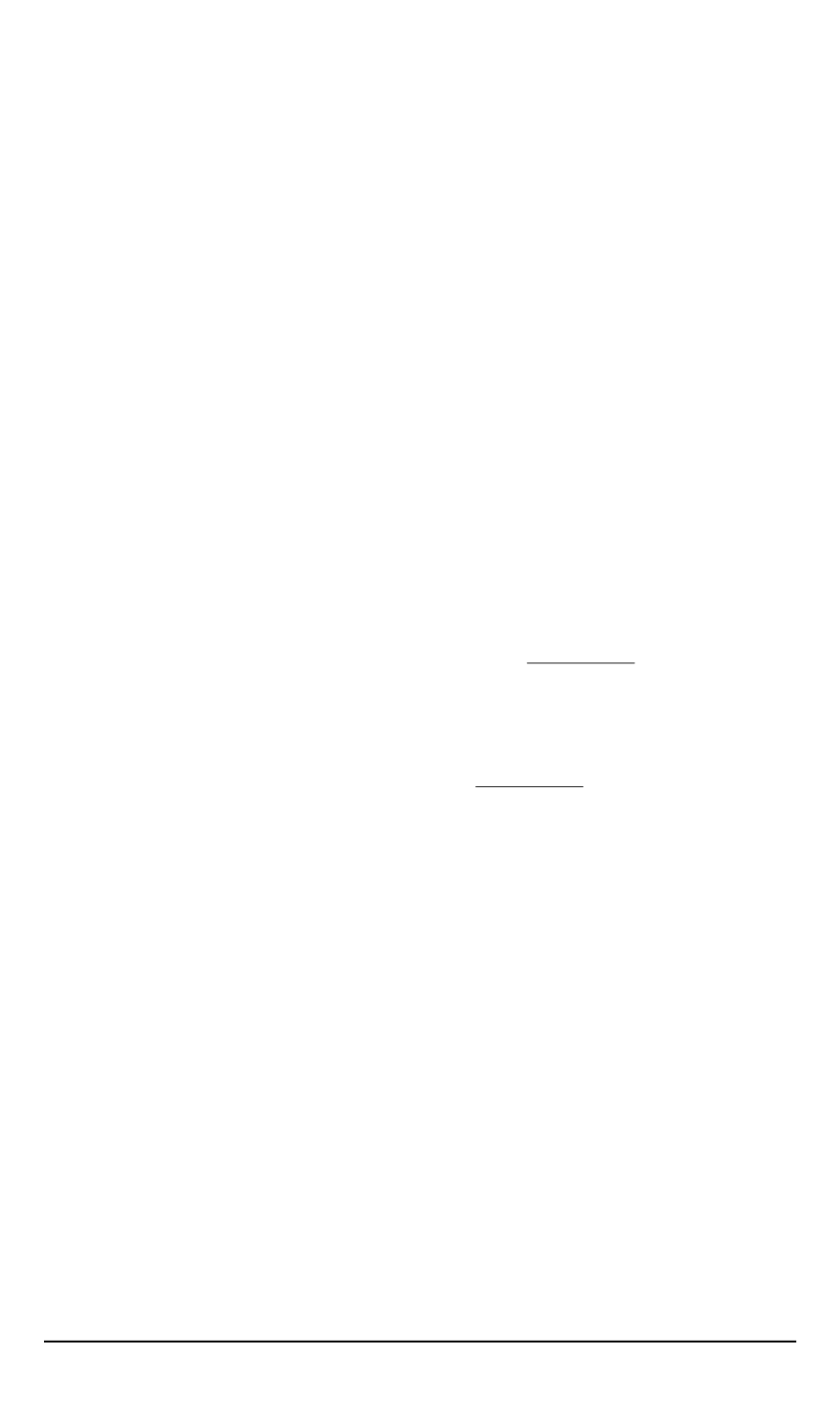
при
α
= (2
,
0)
γ
1
(2
,
1)
=
γ
2
(2
,
0)
,
γ
2
(2
,
1)
=
γ
3
(2
,
0)
,
0 =
¡
γ
1
(0
,
1)
¢
2
+ 2
γ
1
(0
,
2)
γ
1
(0
,
0)
−
γ
4
(0
,
2)
,
0 =
γ
3
(0
,
0)
γ
4
(2
,
0)
+
γ
3
(1
,
0)
γ
4
(1
,
0)
+
γ
3
(2
,
0)
γ
4
(0
,
0)
−
γ
2
(0
,
0)
(
23
)
и т
.
д
.
Подстановка ряда
(22)
в краевые условия
(21)
приводит к квадра
-
тичным уравнениям
γ
1
(0
,
0)
γ
2
(0
,
0)
= 0
,
γ
1
(1
,
0)
γ
2
(0
,
0)
+
γ
1
(0
,
0)
γ
2
(1
,
0)
= 0
,
γ
1
(2
,
0)
γ
2
(0
,
0)
+
γ
1
(1
,
0)
γ
2
(1
,
0)
+
γ
1
(0
,
0)
γ
2
(2
,
0)
=
−
1
,
γ
1
(0
,
0)
γ
2
(3
,
0)
+
γ
1
(3
,
0)
γ
2
(0
,
0)
+
γ
1
(1
,
0)
γ
2
(2
,
0)
+
γ
1
(2
,
0)
γ
2
(1
,
0)
= 0
(
24
)
и т
.
д
.,
являющимся записью условия на стенке
,
уравнениям
N
−
1
X
α
1
+
α
2
=
α
1
γ
1
(
α
1
,α
2
)
= 0
,
α
1
= 0
,
(
N
−
1)
,
(25)
на внешней границе и условию
γ
1
(0
,α
2
)
= 0
,
α
2
= 0
,
(
N
−
1)
,
(26)
в заданном поперечном сечении
.
Решение системы алгебраических
уравнений второго порядка
(23)–(26)
позволяет определить коэффици
-
енты разложения решения задачи
(20)–(21)
в асимптотический ряд
(22).
Представление решения нелинейного уравнения в виде ряда связа
-
но с проблемой выделения из бесконечной системы уравнений конеч
-
ной подсистемы
,
удовлетворительно описывающей свойства решения
,
и разрешения содержащейся в ней нелинейности
.
Отметим работу
[11],
в которой решение уравнений Навье
–
Стокса представляется в виде
функциональных рядов
.
Из бесконечной системы уравнений по некото
-
рому алгоритму выделяют конечную цепочку попарно зацепляющихся
линейных уравнений в частных производных
.
Нелинейность исходных
уравнений последовательно раскрывается в правых частях уравнений
цепочки
.
Предлагаемая процедура
,
по утверждению авторов
,
позволяет
получить всю систему уравнений
,
описывающих нелинейные эффекты
исследуемого течения
.
В отличие от подхода
,
предложенного в рабо
-
те
[11],
в настоящей работе изначально не ставилась цель исключить
62 ISSN 0236-3933.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2004.
№
1