
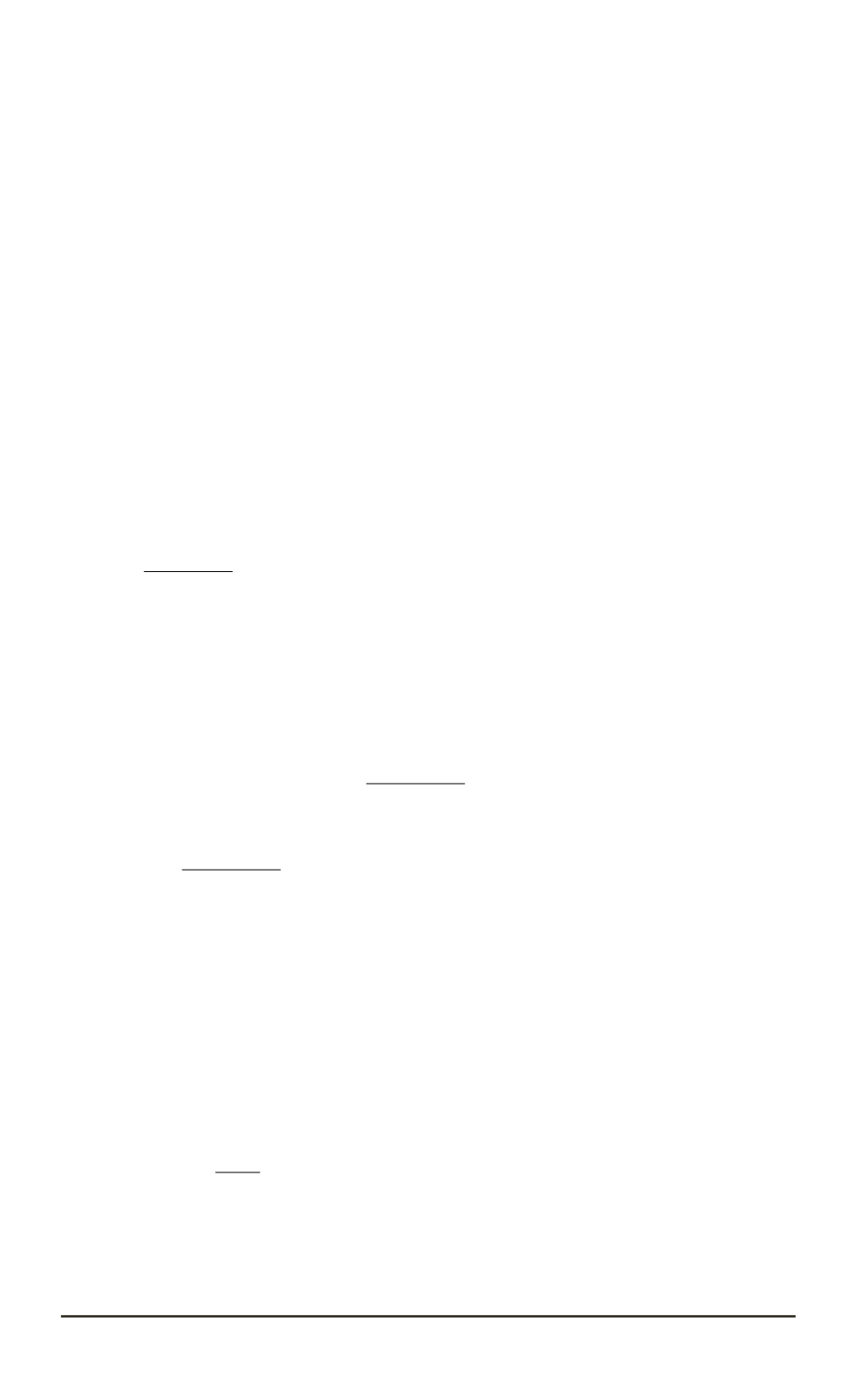
+
Z
Ω
(
g
(
x, t, v
)
−
h
) (
v
−
u
)
dx dt
≥
0
. Возьмем
v
=
u
+
τψ
,
τ >
0
,
ψ
∈
L
r
T
D
(
A
)
:
τ
(
Aψ, ψ
2
) +
Z
Ω
(
g
(
x, t, u
+
τψ
)
−
h
)
ψdx dt
≥
0
.
Устремим
τ
→
0
:
Z
Ω
(
g
(
x, t, u
)
−
h
)
ψdx dt
≥
0
∀
ψ
∈
L
r
(Ω)
T
D
(
A
)
.
Следовательно,
h
=
g
(
x, t, u
)
.
Отсюда и (19) следует, что
u
является
обобщенным решением. Оценка
||
u
||
r
≥
d
вытекает из (5), (18), (22).
Теорема доказана.
Рассмотрим уравнение вынужденных колебаний неоднородной
струны
p
(
x
)
u
tt
−
(
p
(
x
)
u
x
)
x
=
g
(
x, t, u
) +
f
(
x, t
)
,
0
< x < π, t
∈
R.
(23)
Предположим, что нелинейное слагаемое
g
удовлетворяет следующе-
му условию: существуют
α, β
∈
R
,
C
∈
(0
,
+
∞
)
такие, что
α
≤
g
(
x, t, u
)
p
(
x
)
u
≤
β
∀
u
∈
(
−∞
,
−
C
)
[
(
C,
+
∞
)
,
∀
(
x, t
)
∈
Ω
.
(24)
Справедлива следующая теорема.
Tеорема 2.
Пусть
g
∈
C
1
(Ω
×
R
)
,
T
периодична по
t
, выполнены
условия
(4)
,
(7)
и существуют положительные константы
M
1
, M
2
такие, что
|
g
t
(
x, t, u
)
| ≤
M
1
|
u
|
+
M
2
∀
(
x, t, u
)
∈
Ω
×
R
. Предположим,
что либо
B <
0
и выполнено условие
(24)
, в котором
α > B/π
,
[
α, β
]
T
σ
(
A
) =
∅
и
−
γ
≤
g
u
(
x, t, u
)
p
(
x
)
≤
M
3
∀
(
x, t, u
)
∈
Ω
×
R
, либо
B >
0
и выполнено условие
(24)
, где
β < B/π
,
[
−
β,
−
α
]
T
σ
(
A
) =
∅
и
−
γ
≤ −
g
u
(
x, t, u
)
p
(
x
)
≤
M
3
∀
(
x, t, u
)
∈
Ω
×
R
,
M
3
>
0
,
γ
∈
(0
,
|
B
|
/π
)
.
Тогда для любой функции
f
(
x, t
)
∈
H
1
(Ω)
задача
(2)
,
(3)
,
(23)
имеет
обобщенное решение
u
∈
H
0
1
(Ω)
.
Доказательство существования решения опирается на теорему 3.1,
приведенную в работе [10], доказательство гладкости решения дано в
работе [15].
Замечание.
Полученное в теореме 2 решение будет единственно,
если дополнительно условиям этой теоремы потребовать при
B <
0
выполнения условия
α
(
u
−
v
)
2
≤
1
p
(
x
)
(
g
(
x, t, u
)
−
g
(
x, t, v
))(
u
−
v
)
≤
≤
β
(
u
−
v
)
2
∀
u, v
∈
R,
∀
(
x, t
)
∈
Ω
,
а при
B >
0
— условия
12
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 4

















