
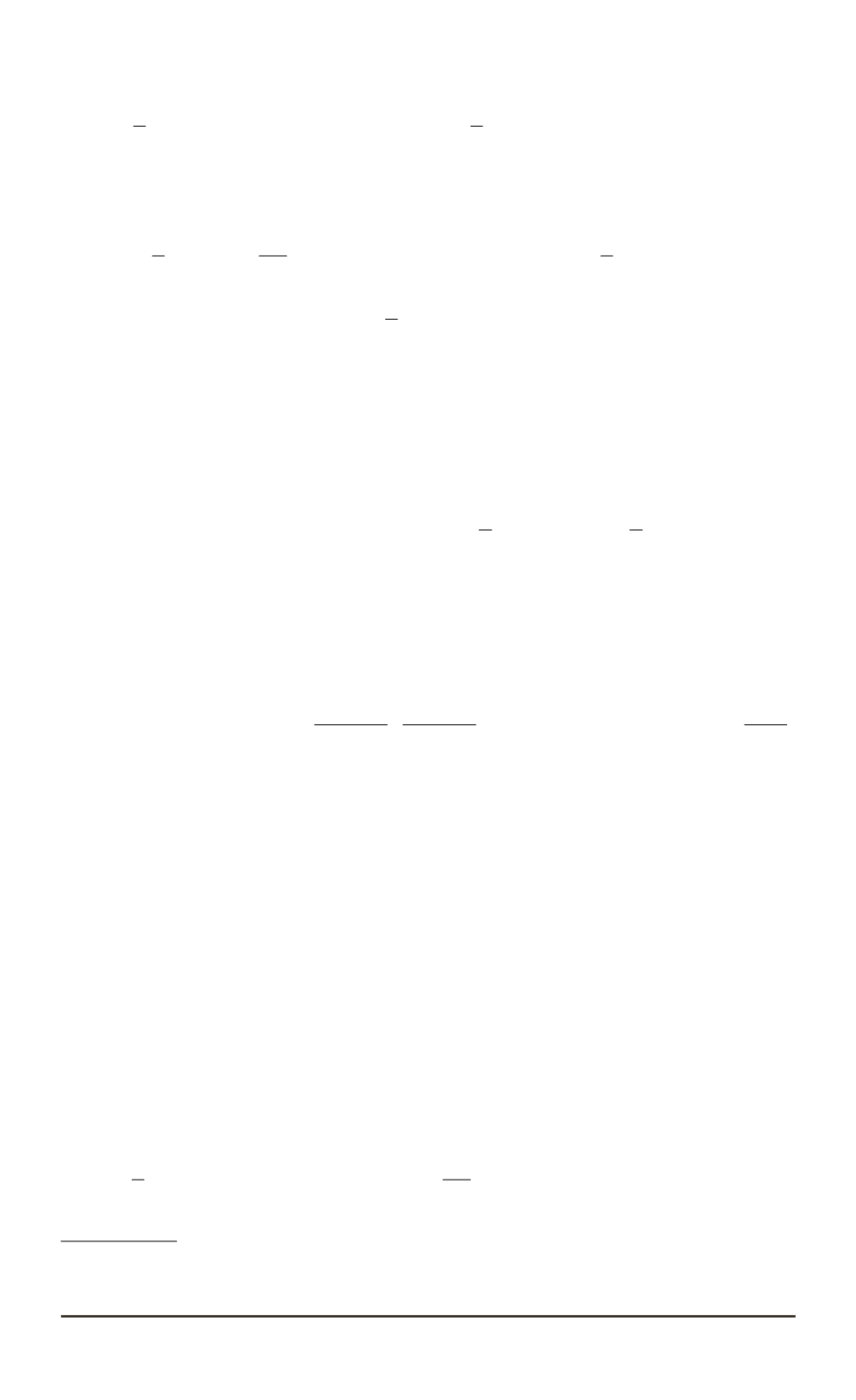
ми или не меньшими
c
. Из условия (5) выведем
∗∗
1
r
A
3
|
u
|
r
−
A
5
|
u
| ≤
G
(
x, t, u
)
≤
1
r
A
1
|
u
|
r
+
A
2
|
u
| ∀
x, t, u.
Поэтому для любого действительного
c >
0
и любой функции
u
∈
G
c
получим
F
(
u
)
≥
1
2
c
||
u
||
2
+
A
3
r
||
u
||
r
r
−
A
5
||
u
||
L
1
≥
A
6
||
u
||
r
−
1
2
|
c
|||
u
||
2
−
A
7
||
u
||
.
Обозначим
h
(
τ
) =
A
6
τ
r
−
1
2
|
c
|
τ
2
−
A
7
τ
. Функция
h
(
τ
)
ограни-
чена снизу и
h
(
τ
)
→
+
∞
при
τ
→
+
∞
. Поэтому существует
m
(
c
) = min
[0
,
+
∞
)
h
(
τ
)
−
1
.
Следовательно,
F
(
u
)
> m
(
c
)
∀
u
∈
G
c
.
(11)
Разложим функцию
u
∈
E
n
в ряд Фурье:
u
=
X
(
n,m
)
∈
N
×
Z
+
ϕ
n
(
x
)
a
nm
cos
a
b
mt
+
b
nm
sin
a
b
mt .
Обозначим
|||
u
|||
s
=
X
(
n,m
)
∈
N
×
Z
+
|
μ
nm
|
s
a
2
nm
+
b
2
nm
.
Возьмем число
α
∈
r
−
2
2(
r
−
1)
,
r
2(
r
−
1)
и обозначим
β
= 2
α
r
−
1
r
.
Используя неравенство Хаусдорфа –Юнга и Гельдера, выведем
||
u
||
r
≤
C
1
|||
u
|||
β
∀
u
∈
H
3
n
.
(12)
Обозначим
S
n
=
u
∈
E
n
|||
u
|||
β
= 1
.
Лемма 1.
Для любого действительного числа
d
существует число
w
(
d
)
<
0
такое, что
F
(
u
)
≤
d
∀
u
∈ {
v
∈
L
w
(
d
)
||||
v
|||
β
= 1
}
.
J
Пусть
w <
0
. На множестве
N
2
n
собственные значения оператора
А
положительные. Следовательно,
L
ω
⊆
N
3
n
. Пусть
u
∈
L
ω
T
S
n
,
a
mk
, b
mk
— коэффициенты фурье-функции
u
. Используя (12), выведем
существование константы
C >
0
такой, что
F
(
u
)
≤
≤ −
1
2
X
(
m,k
)
∈
M
|
μ
mk
|
a
2
mk
+
b
2
mk
+
A
1
r
Z
Ω
|
u
|
r
dxdt
+
A
2
Z
Ω
|
u
|
dxdt
≤
∗∗
Здесь и далее буквами с индексами
A
1
, A
2
, . . .
;
C
1
, C
2
, . . .
обозначим положи-
тельные константы.
8
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 4

















