
Здесь
V
0
=
U
0
2
λ
(
A
0
+
C
0
)
;
ε
=
A
0
+
C
0
8
λ
E
;
Λ
λ
=
Λ
2
λ
.
Отметим, что
параметр
ν
определяет эллиптичность линий уровня потенциальной
ямы.
Поскольку отображение
(
ρ, ϕ
)
→
(
x
1
, x
2
)
обладает особенностью
при
ρ
= 0
,
ϕ
∈
[0
,
2
π
]
, для обеспечения дважды непрерывной диф-
ференцируемости волновой функции
ψ
(
x
1
, x
2
)
на функции
ψ
1
(
ϕ
)
,
ψ
2
(
ρ
)
следует наложить дополнительные условия. Для того чтобы
ψ
(
x
1
, x
2
)
∈
C
2
необходимо и достаточно выполнения одного из двух
условий:
1)
ψ
1
(0) =
ψ
1
(
π
) = 0
, ψ
2
(0) = 0;
(9)
2)
dψ
1
dϕ
ϕ
=0
=
dψ
1
dϕ
ϕ
=
π
= 0
,
dψ
2
dρ
ρ
=0
= 0
.
(10)
При выполнении условий (9) или (10) функция
ψ
1
(
ϕ
)
будет
2
π
-
периодической.
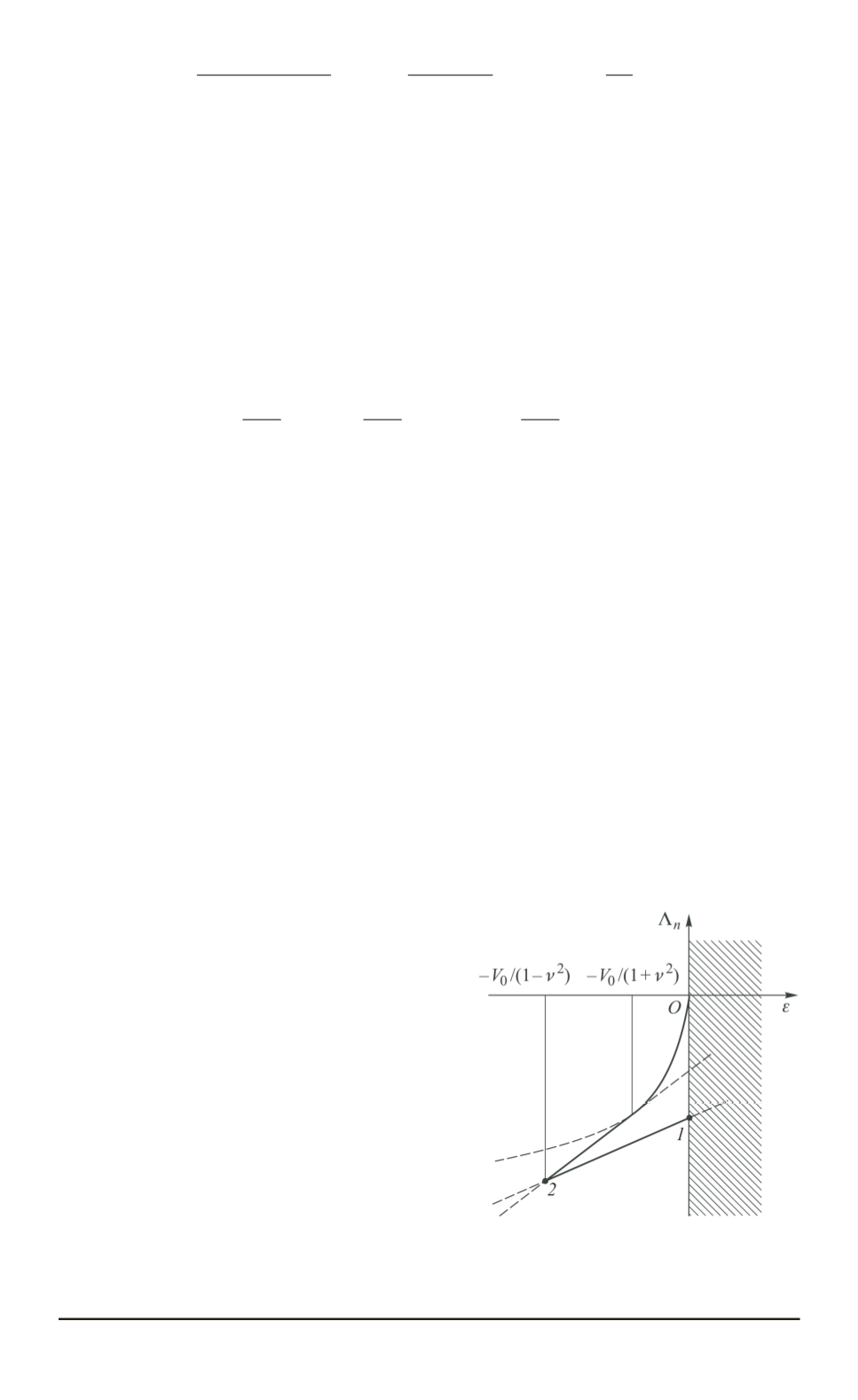
Качественный анализ спектра собственных значений одномер-
ных задач (8) с учетом возможностей продолжения решений на всю
плоскость
(
x
1
, x
2
)
привел к структуре спектра двумерной задачи,
изображенной на рисунке. В области
О12
точки пересечения двух
семейств кривых
Λ = Λ
(
i
)
n
(
ε
)
, монотонно возрастающих с увеличени-
ем значения
ε
, определяют точечный спектр двумерной задачи. Точ-
ке
2
, ограничивающей точечный спектр снизу, соответствует значение
ε
=
−
V
0
/ (1
−
ν
2
)
, совпадающее с простой оценкой энергии основного
состояния по глубине потенциальной ямы. Сплошной спектр распо-
ложен в заштрихованной области. Для собственных значений
Λ
(
i
)
n
(
ε
)
справедливо неравенство
d
Λ
(1)
n
−
Λ
(2)
m
.
dε <
0
, означающее, что
Структура спектра двумерной за-
дачи
на плоскости
(Λ
, ε
)
кривые
Λ
(
i
)
n
(
ε
)
пересекаются трансверсально при
ε <
0
. Можно предположить, что
Λ
(2)
n
(
ε
)
→
0
при
ε
→
0
со стороны
отрицательных значений. Такое пред-
положение связано с тем, что потен-
циальная яма с асимптотикой (5) при-
водит к счетному множеству точек то-
чечного спектра, обладающих точкой
сгущения
ε
= 0
. При заданных значе-
ниях параметров двумерной ямы
V
0
,
ν
с семейством кривых
Λ
(2)
n
(
ε
)
мо-
жет пересечься только конечное число
кривых семейства
Λ
(1)
n
(
ε
)
и это число
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 6
9
















