
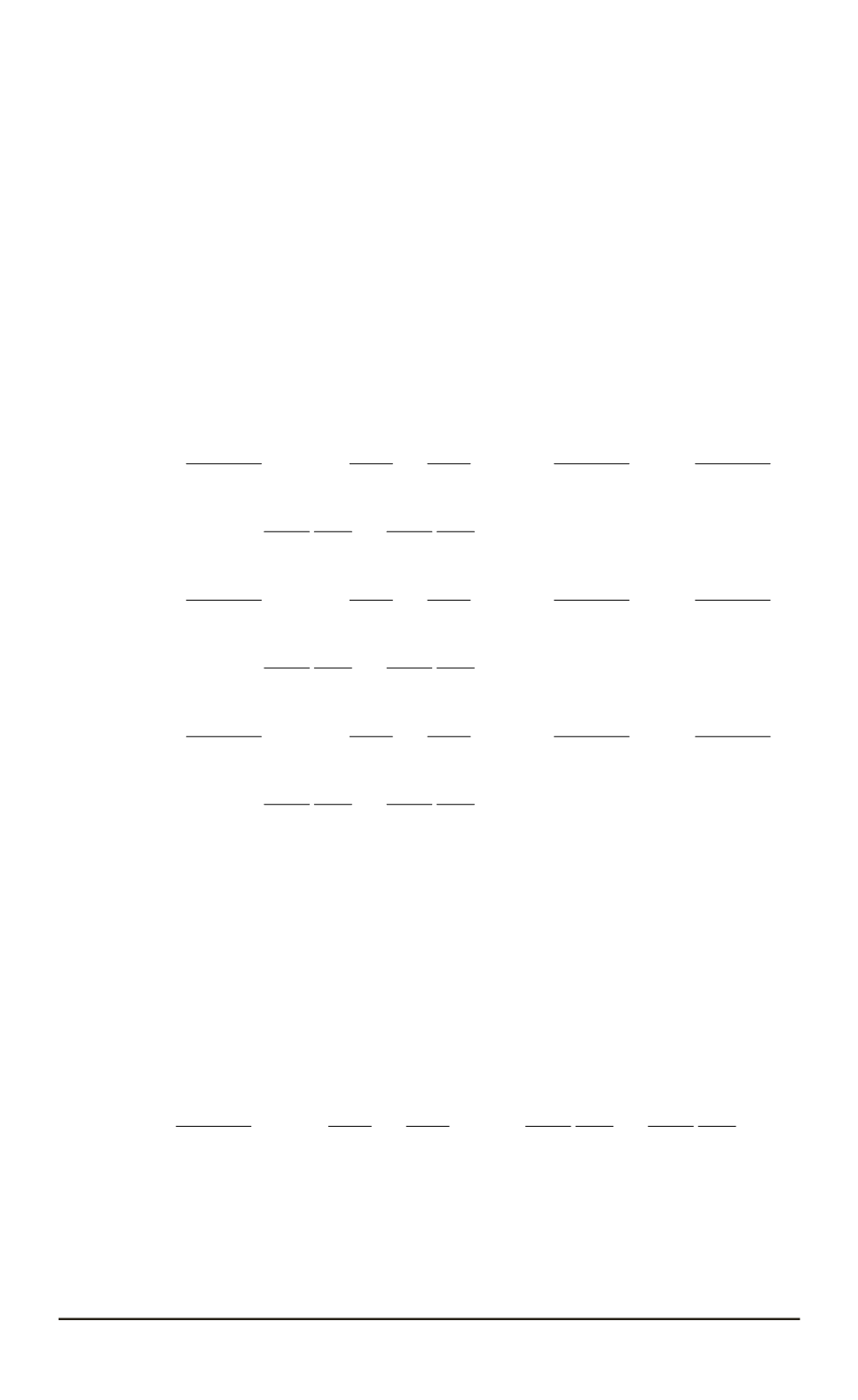
a
11
=
A
22
x
2
2
+
A
33
x
2
3
+
A
2
x
2
+
A
3
x
3
+
a
0
11
;
a
22
=
A
22
x
2
1
+
B
33
x
2
3
+
B
1
x
1
+
B
3
x
3
+
a
0
22
;
a
33
=
A
33
x
2
1
+
B
33
x
2
2
+
C
1
x
1
+
C
2
x
2
+
a
0
33
;
2
a
12
=
−
2
A
22
x
1
x
2
−
A
2
x
1
−
B
1
x
2
+ 2
a
0
12
;
2
a
13
=
−
2
A
33
x
1
x
3
−
A
3
x
1
−
C
1
x
3
+ 2
a
0
13
;
2
a
23
=
−
2
B
33
x
2
x
3
−
B
3
x
2
−
C
2
x
3
+ 2
a
0
23
.
(13)
Условия разрешимости соотношений (12) приводят к трем уравне-
ниям для потенциала
(
a
11
−
a
22
)
∂
2
U
∂x
1
∂x
2
−
a
12
∂
2
U
∂x
2
1
−
∂
2
U
∂x
2
2
+
a
13
∂
2
U
∂x
2
∂x
3
−
a
23
∂
2
U
∂x
1
∂x
3
−
−
3
∂a
12
∂x
1
∂U
∂x
1
−
∂a
12
∂x
2
∂U
∂x
2
= 0;
(
a
11
−
a
33
)
∂
2
U
∂x
1
∂x
3
−
a
13
∂
2
U
∂x
2
1
−
∂
2
U
∂x
2
3
+
a
12
∂
2
U
∂x
2
∂x
3
−
a
23
∂
2
U
∂x
1
∂x
2
−
−
3
∂a
13
∂x
1
∂U
∂x
1
−
∂a
13
∂x
3
∂U
∂x
3
= 0;
(
a
22
−
a
33
)
∂
2
U
∂x
2
∂x
3
−
a
23
∂
2
U
∂x
2
2
−
∂
2
U
∂x
2
3
+
a
12
∂
2
U
∂x
1
∂x
3
−
a
13
∂
2
U
∂x
1
∂x
2
−
−
3
∂a
23
∂x
2
∂U
∂x
2
−
∂a
23
∂x
3
∂U
∂x
3
= 0
.
Очевидно, что предположение о существовании одного дополни-
тельного интеграла вида (12) вместо двух необходимых для полной ин-
тегрируемости в случае трех степеней свободы приводит к переопре-
деленной системе уравнений для одной функции трех переменных. В
качестве простого примера рассмотрим случай, когда
a
13
=
a
23
= 0
.
Система (14) допускает решения вида
U
(
x
1
, x
2
, x
3
) =
U
(
x
1
, x
2
) +
+
u
(
x
3
)
. При этом
u
(
x
3
)
— произвольно, а
U
(
x
1
, x
2
)
— решение урав-
нения
(
a
11
−
a
22
)
∂
2
U
∂x
1
∂x
2
−
a
12
∂
2
U
∂x
2
1
−
∂
2
U
∂x
2
2
−
3
∂a
12
∂x
1
∂U
∂x
1
−
∂a
12
∂x
2
∂U
∂x
2
= 0
,
исследованного ранее в работе [6]. В качестве следующего примера
рассмотрим задачу о парном взаимодействии трех точек на прямой.
Пусть
U
(
x
1
, x
2
, x
3
) =
U
12
(
x
1
−
x
2
) +
U
13
(
x
1
−
x
3
) +
U
23
(
x
2
−
x
3
)
(14)
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 6
11
















