
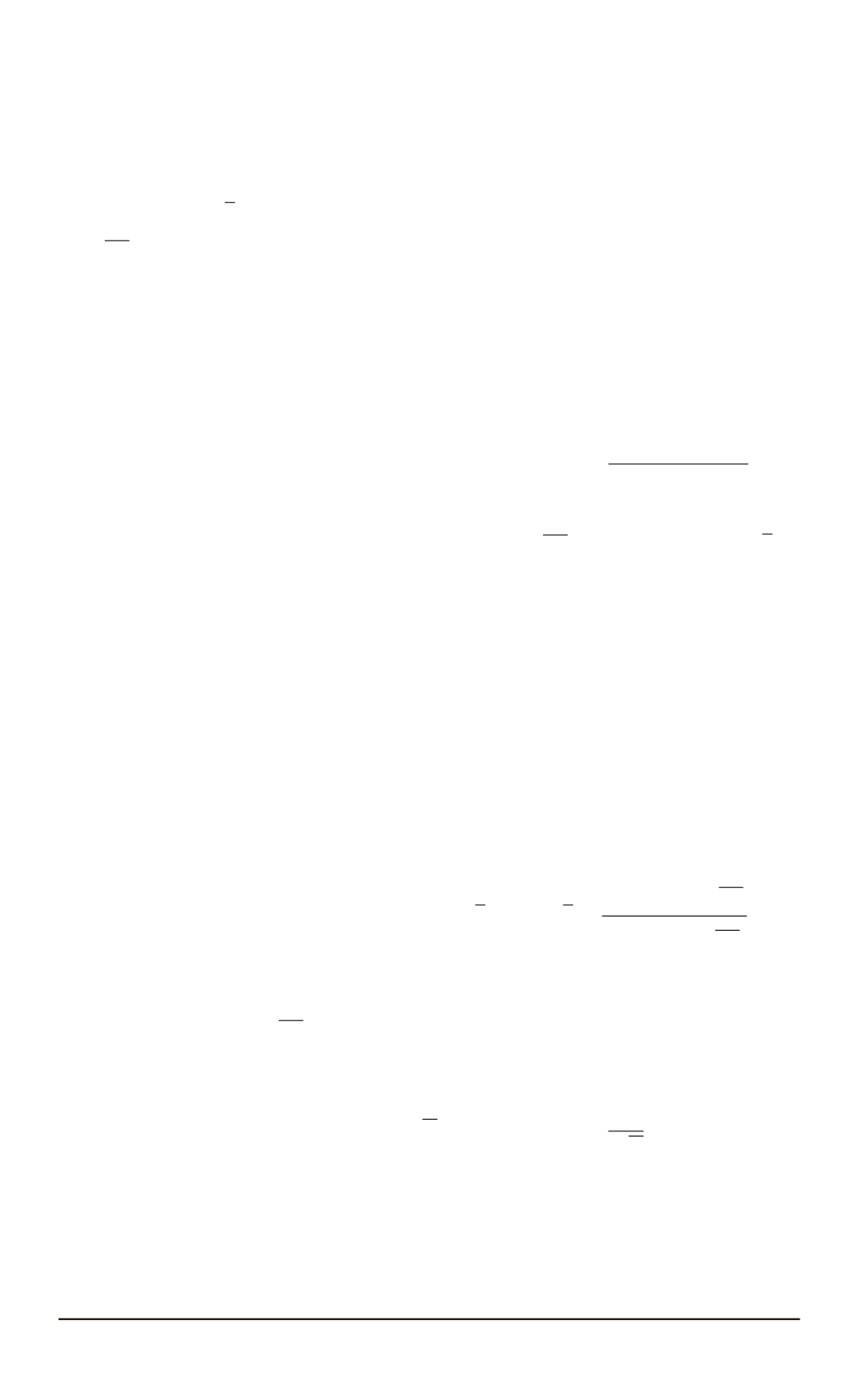
Асимптотическое распределение
T
.
Вид предлагаемой статисти-
ки
T
связан с тем, что ее асимптотическое распределение может быть
приближено классическим распределением Колмогорова – Смирнова.
Без ограничения общности можно полагать, что
P
1
(
t
) = 1
−
t,
P
2
(
t
) = (1
−
t
)
1
k
,
0
≤
t
≤
1
. Рассмотрим сначала процесс
X
1
(
t
) =
=
√
n
1
_
P
θ
1
(
t
)
−
(1
−
t
)
. В работе [2] была доказана следующая те-
орема, дающая выражение для асимптотической ковариации процесса
X
1
(
t
)
.
Теорема 4.
Пусть
0
≤
s
≤
t
≤
Δ
<
1
,
тогда
K
1
(
s, t
) =
EX
1
(
s
)
X
1
(
t
)
−
−
EX
1
(
s
)
EX
1
(
t
)
−→
n
1
∞
(1
−
t
)(1
−
s
)
1
−
(1
−
s
)
m
1
m
2
1
(1
−
s
)
m
1
.
Далее рассмотрим процесс
˜
X
2
(
t
) =
√
n
2
_
P
θ
2
(
t
)
−
(1
−
t
)
1
k
,
0
≤
t
≤
1
.
Метод получения асимптотической ковариации процесса
˜
X
2
(
t
)
полностью аналогичен методу определения ковариации
X
1
(
t
)
, при-
веденному в работе [2], и поэтому вид асимптотической ковариации
˜
K
2
(
s, t
) =
E
˜
X
2
(
s
) ˜
X
2
(
t
)
−
E
˜
X
2
(
s
)
E
˜
X
2
(
t
)
приводится без доказа-
тельства.
Теорема 5.
Пусть
0
≤
s
≤
t
≤
Δ
<
1
,
тогда
˜
K
2
(
s, t
) =
E
˜
X
2
(
s
) ˜
X
2
(
t
)
−
−
E
˜
X
2
(
s
)
E
˜
X
2
(
t
)
−→
n
2
→∞
(1
−
t
)
1
k
(1
−
s
)
1
k
1
−
(1
−
s
)
m
2
k
m
2
2
(1
−
s
)
m
2
k
!
.
Для того чтобы получить асимптотическую функцию ковариации
процесса
X
2
(
t
) =
√
n
2
_
P
θ
2
(
t
)
k
−
(1
−
t
)
,
0
≤
t
≤
1
, воспользу-
емся следующим результатом [11].
Теорема 6.
Пусть
h
n
(
x
) =
√
n
(1
−
t
)
1
/k
+
x
√
n
k
−
(1
−
t
)
!
,
h
(
x
) =
k
(1
−
t
)
1
−
1
/k
x, x
∈
D
[0
,
1]
, D
[0
,
1]
— пространство функций
без разрывов второго рода на
[0
,
1]
. Тогда последовательность
h
n
(
x
)
сходится в метрике Скорохода к
h
(
x
)
равномерно на ограниченных
множествах из
D
[0
,
1]
.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 6
77
















