
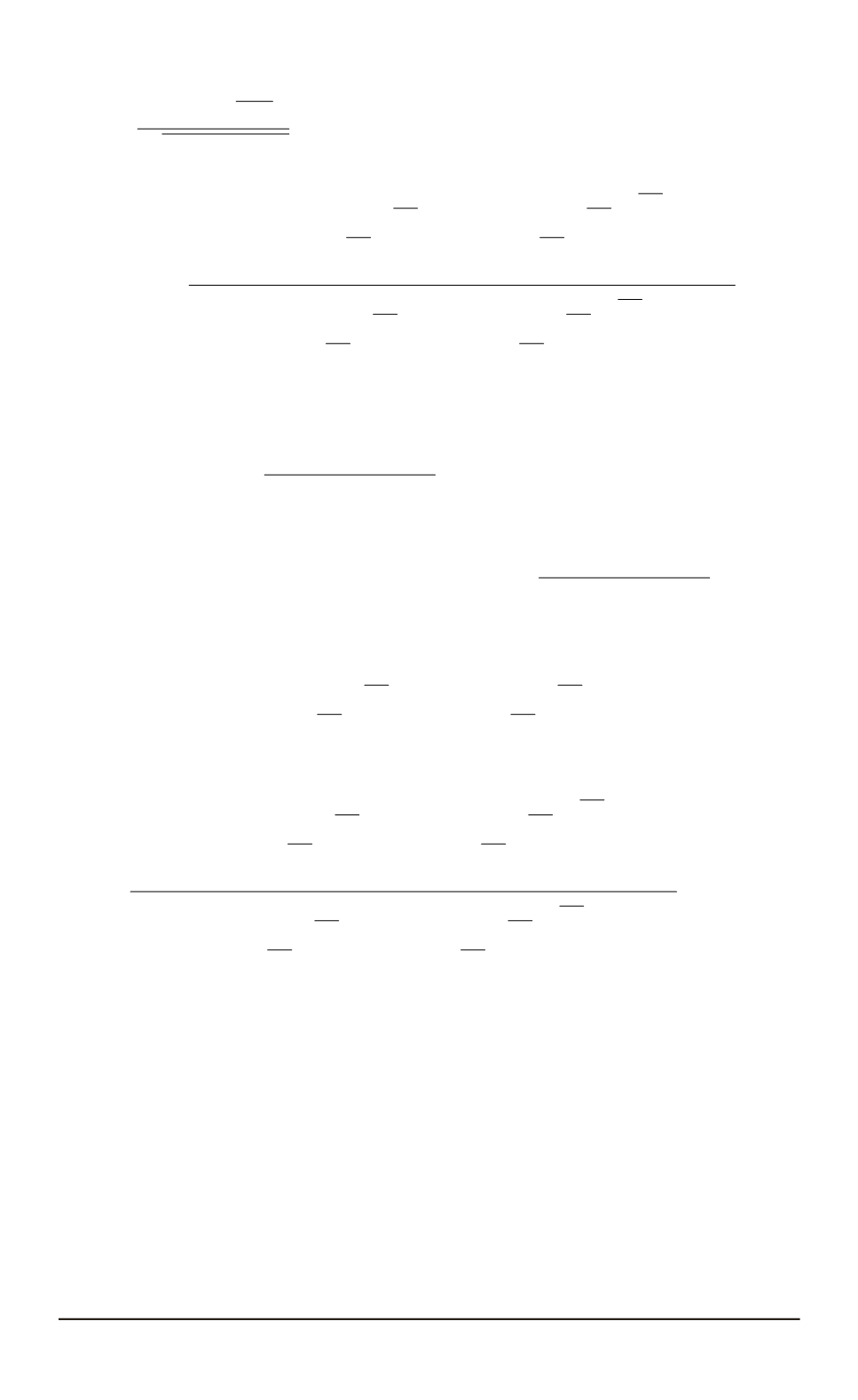
принимает значение
t
ij
, равное
t
ij
=
m
1
m
2
√
ρn
2
p
k
2
ρm
2
1
+
m
2
2
×
×
k
2
1
−
i
n
1
1
m
1
+
k
1
1
−
j
n
2
k
m
2
m
2
k
−
1
k
2
k
2
1
−
i
n
1
1
m
1
+
k
1
1
−
j
n
2
k
m
2
m
2
k
−
m
1
+
k
1
Δ
ij
,
где
Δ
ij
=
i
Y
s
1
=1
1
−
1
m
1
(
n
1
−
s
1
+ 1)
−
−
j
Y
s
2
=1
1
−
1
m
2
(
n
2
−
s
2
+ 1)
!
k
.
При этом для
m
2
/k
−
1
<
0
и
k
2
1
−
i
n
1
1
m
1
+
k
1
1
−
j
n
2
k
m
2
= 0
сохраняется условие
k
2
1
−
i
n
1
1
m
1
+
k
1
1
−
j
n
2
k
m
2
m
2
k
−
1
k
2
k
2
1
−
i
n
1
1
m
1
+
k
1
1
−
j
n
2
k
m
2
m
2
k
−
m
1
+
k
1
= 0
.
Отметим, что параметр
t
ij
не зависит от траектории частицы. Осно-
вываясь на описанной модели случайного блуждания предложен метод
вычисления точных распределений статистики
T
[9].
Теорема 3.
Вероятность
P
{
T < h
}
равна
π
n
1
,n
2
(
h
)
,
которую
можно получить повторным применением соотношения
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 6
75
















