
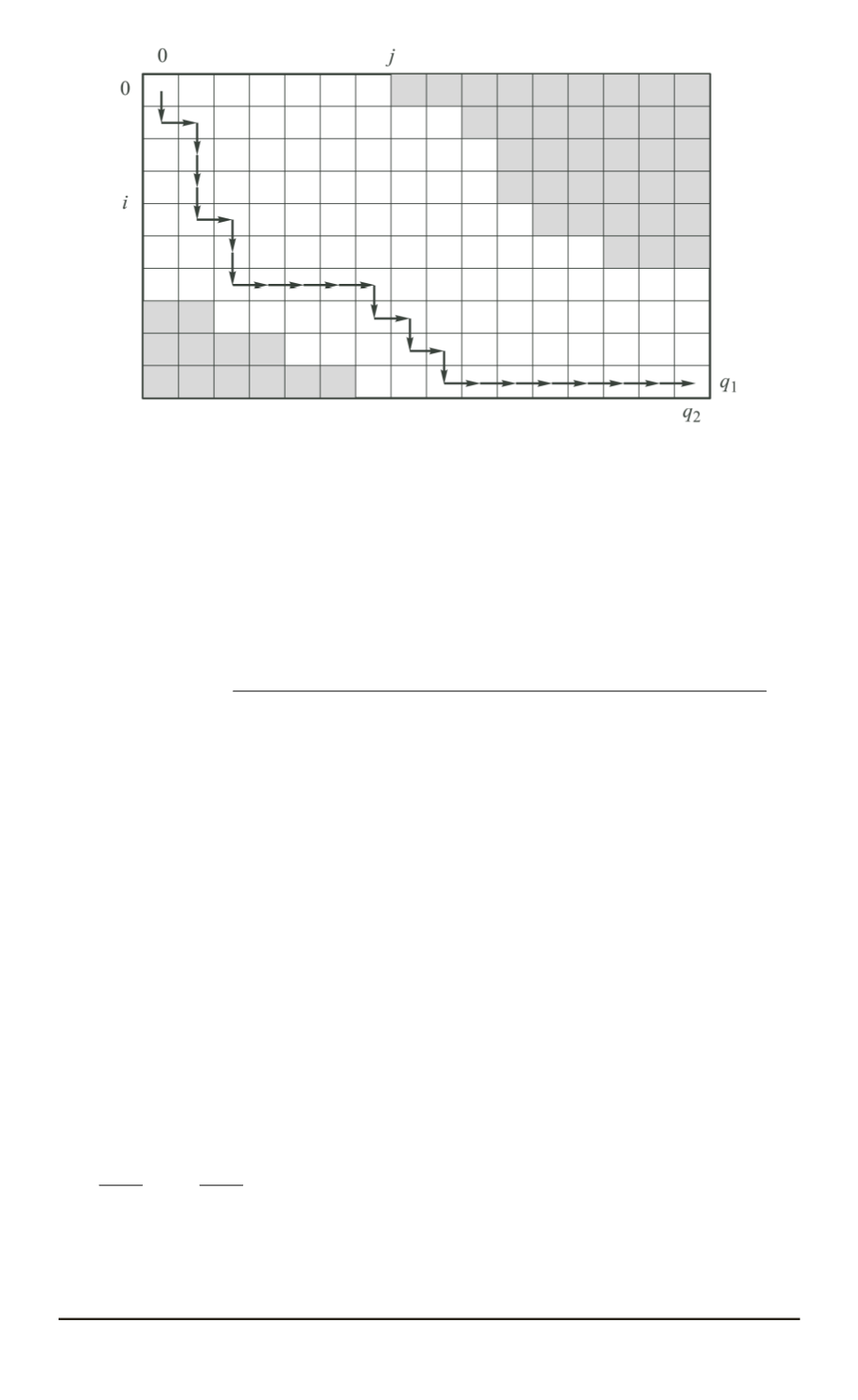
Рис. 1. Схема массива ячеек, по которым происходит случайное блуждание ча-
стицы
Теорема 1.
Распределение вероятностей вектора
−→
Z
= (
z
1
, z
2
, . . .
. . . , z
q
1
+
q
2
)
определяется по следующему выражению
:
p
−→
Z
=
q
1
+
q
2
Y
s
=1
N
1
−
V
s
−
1
X
l
=1
r
1
l
−
V
s
−
1
!
k
!
z
s
N
2
−
U
s
−
1
X
l
=1
r
2
l
−
U
s
−
1
!
1
−
z
s
N
1
−
V
s
−
1
X
l
=1
r
1
l
−
V
s
−
1
!
k
+
N
2
−
U
s
−
1
X
l
=1
r
2
l
−
U
s
−
1
,
где
V
j
=
j
X
i
=1
z
i
,
V
0
= 0
—
число единиц в векторе
−→
Z
до
j
-го места
включительно
;
U
j
=
j
−
j
X
i
=1
z
i
,
U
0
= 0
—
число нулей в векторе
−→
Z
до
j
-го места включительно
.
J
Утверждение теоремы следует из вида условных вероятностей
перехода “вниз” или “вправо” в схеме случайного блуждания частицы
[9, 10].
I
Обозначим через
P
вероятность невыхода траектории случайно-
го блуждания из некоторого подмножества
A
0
множества
{
a
ij
}
=
A
,
i
= 0
, q
1
,
j
= 0
, q
2
.
Теорема 2.
Вероятность
P
равна
π
q
1
,q
2
,
которую можно получить
повторным применением соотношения
72
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 6
















