
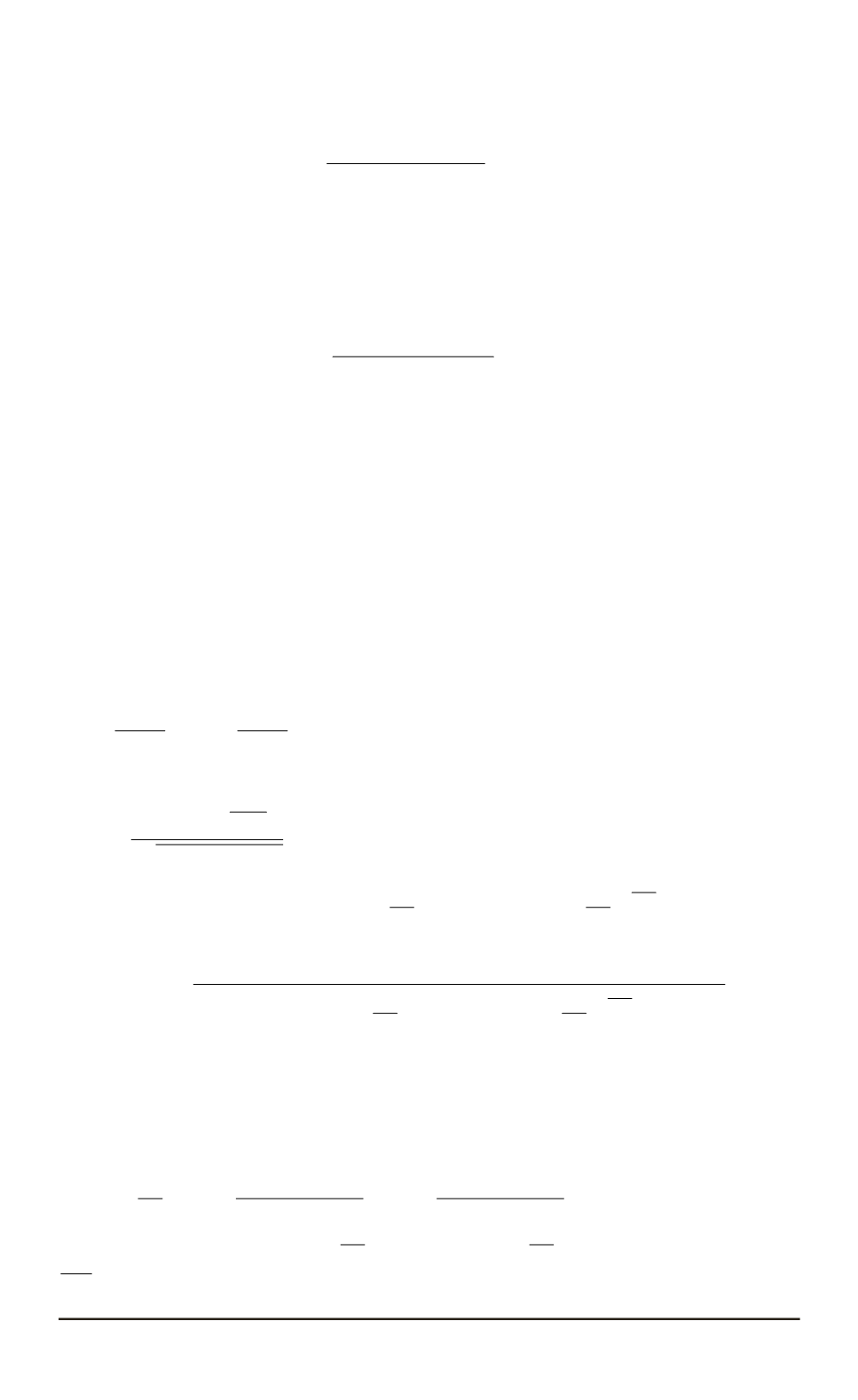
_
P
θ
1
(
t
) =
1
, d
1
(
t
) = 0
,
d
1
(
t
)
Y
i
=1
1
−
1
m
1
(
n
1
−
i
+ 1)
,
1
≤
d
1
(
t
)
≤
(
n
1
−
1)
,
0
, d
1
(
t
) =
n
1
;
_
P
θ
2
(
t
) =
1
, d
2
(
t
) = 0
,
d
2
(
t
)
Y
j
=1
1
−
1
m
2
(
n
2
−
j
+ 1)
,
1
≤
d
2
(
t
)
≤
(
n
2
−
1)
,
0
, d
2
(
t
) =
n
2
.
Здесь
d
1
(
t
)
, d
2
(
t
)
— число элементов выборок
Θ
1
и
Θ
2
, меньших зна-
чения
t
.
Отметим, что выборки
(
θ
1
1
, . . . , θ
n
1
1
)
,
(
θ
1
2
, . . . , θ
n
2
2
)
можно рассматри-
вать и как полные (нецензурированные) независимые выборки из сово-
купностей с функциями распределения
F
1
(
t
) = 1
−
(
P
1
(
t
))
m
1
, F
2
(
t
) =
= 1
−
(
P
2
(
t
))
m
2
. При этом функции распределения
F
1
(
t
)
, F
2
(
t
)
мож-
но оценить обычными эмпирическими функциями распределения
_
F
1
=
d
1
(
t
)
n
1
,
_
F
2
=
d
2
(
t
)
n
2
.
Для проверки гипотезы (1) предложена статистика вида
T
=
m
1
m
2
√
ρn
2
p
k
2
ρm
2
1
+
m
2
2
×
×
max
t
k
2
1
−
_
F
1
1
m
1
+
k
1
1
−
_
F
2
k
m
2
m
2
k
−
1
k
2
k
2
1
−
_
F
1
1
m
1
+
k
1
1
−
_
F
2
k
m
2
m
2
k
−
m
1
+
k
1
×
×
_
P
θ
1
(
t
)
−
_
P
θ
2
(
t
)
k
,
(2)
где
ρ
=
n
1
n
2
;
k
2
=
m
2
2
ρm
2
1
k
2
+
m
2
2
;
k
1
=
ρm
2
1
k
2
ρm
2
1
k
2
+
m
2
2
. При этом для случая
m
2
k
−
1
<
0
и
k
2
1
−
_
F
1
1
m
1
+
k
1
1
−
_
F
2
k
m
2
= 0
примем
70
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 6
















