
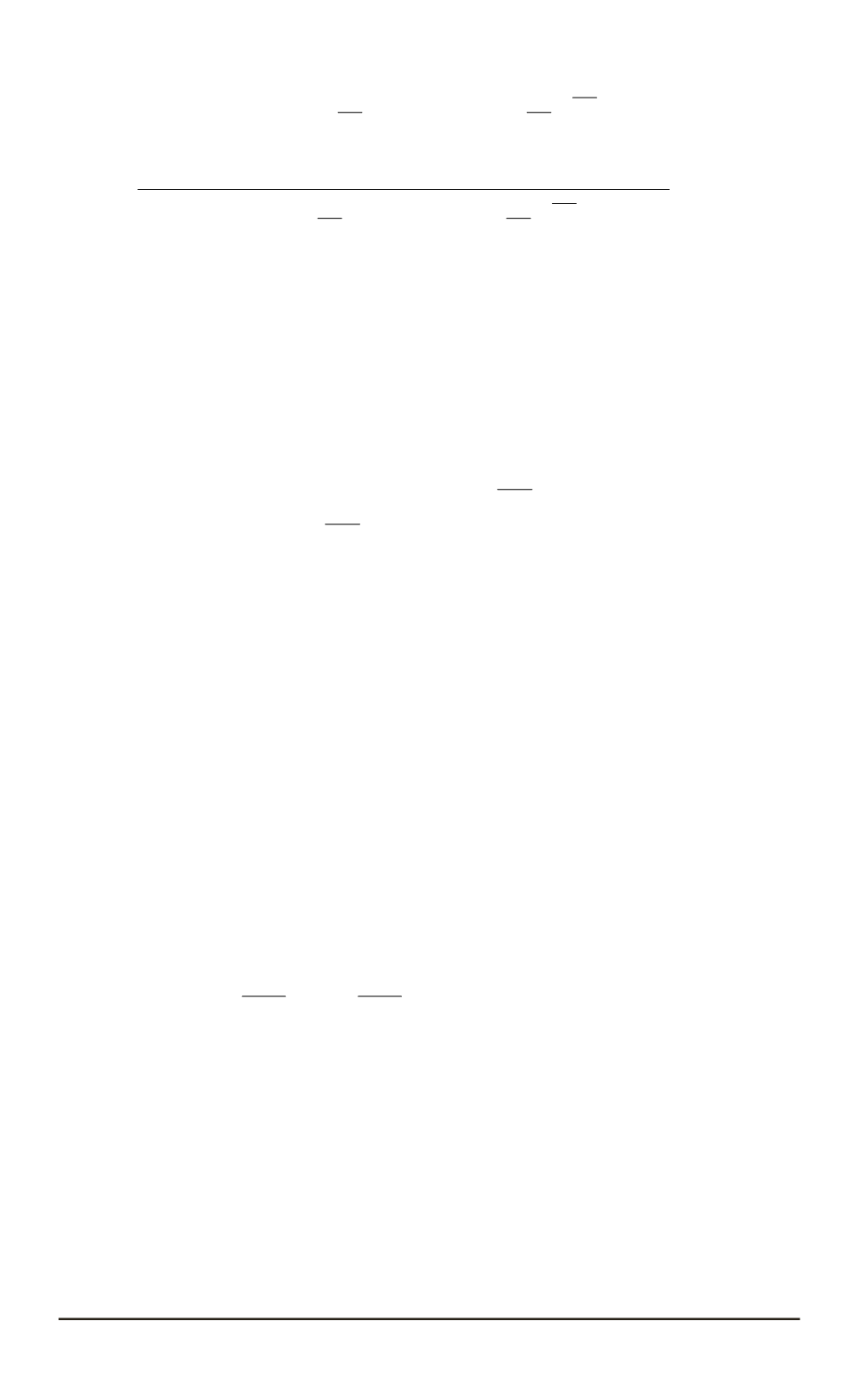
k
2
1
−
_
F
1
1
m
1
+
k
1
1
−
_
F
2
k
m
2
m
2
k
−
1
k
2
k
2
1
−
_
F
1
1
m
1
+
k
1
1
−
_
F
2
k
m
2
m
2
k
−
m
1
+
k
1
= 0
.
Точные распределения
T
.
Для вычисления точных распределе-
ний статистики (2) рассмотрим более общую постановку задачи. Пусть
испытания проводят следующим образом. Имеется два режима рабо-
ты: в режиме
ε
1
работает
N
1
элементов, в режиме
ε
2
—
N
2
элементов.
При
i
-м отказе одного из изделий в режиме
ε
1
с испытаний снима-
ются (цензурируются)
r
1
i
изделий
(
i
= 1
, q
1
)
, в режиме
ε
2
при
j
-м
отказе —
r
2
j
изделий
(
j
= 1
, q
2
)
. Такая схема цензурирования называет-
ся прогрессивным цензурированием [4, 7, 8], причем
N
1
=
q
1
X
i
=1
r
1
i
+
q
1
,
N
2
=
q
2
X
j
=1
r
2
j
+
q
2
. По результатам испытаний имеется две прогрессивно
цензурированные выборки
Q
1
, Q
2
объемами
q
1
, q
2
. Уточним, что пара-
метры
r
1
i
, r
2
j
известны заранее и не являются случайными величинами.
Введем вектор
−→
Z
= (
z
1
, z
2
, . . . , z
q
1
+
q
2
)
, который состоит из
q
1
еди-
ниц и
q
2
нулей, причем
z
i
=
(
1
,
если отказ из выборки
Q
1
,
0
,
если отказ из выборки
Q
2
,
i
= 1
, . . . ,
(
q
1
+
q
2
)
.
Рассмотрим следующую модель случайного блуждания [9]. Пусть
{
a
ij
}
=
A
,
i
= 0
, q
1
,
j
= 0
, q
2
— двумерный массив ячеек. Части-
ца на первом шаге выходит из ячейки
a
0
,
0
и на
(
q
1
+
q
2
)
-м шаге за-
канчивает блуждание в ячейке
a
q
1
,q
2
, совершая
q
1
скачков “вниз” и
q
2
скачков “вправо”. Траектории частицы будут находиться во вза-
имно однозначном соответствии с вектором
−→
Z
. Равенство
z
k
= 1
,
k
= 1
, . . . ,
(
q
1
+
q
2
)
, в векторе
−→
Z
соответствует скачку “вниз” на
k
-м
шаге, появление
z
k
= 0
,
k
= 1
, . . . ,
(
q
1
+
q
2
)
— скачку “вправо”. Схема
массива ячеек, по которым происходит случайное блуждание частицы,
показана на рис. 1.
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2015. № 6
71
















