
Нахождение эффективной теплопроводности композита методом моментов
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2016. № 4
31
Применим метод Фурье. Для теплоизолированных поверхностей граничные
условия
(0, ) = ( , ) = 0,
x
x
u t u b t
следовательно, в гильбертовом пространстве
2
[0, ]
L b
необходимо взять следующий ортонормированный базис:
0
1
2
( ) = , ( ) = cos
, =1, 2, 3,
n
nx
f x
f x
n
b
b
b
(3)
Разложим дельта-функцию
( )
x
по базису (3):
0
,
=1 , < ,
>= 2 ,
n
f
b
f
b
следовательно,
=0
=1
1
( )
< ,
> ( ) = 1 2 cos
.
n n
n
n
nx
x
f
f x
b
b
При
> 0
t
из уравнения теплопроводности
2
= =
xx
u a u au
получаем
2 2
2
=1
1
( , ) = 1 2 cos
exp
.
n
nx
n at
u x t
b
b
b
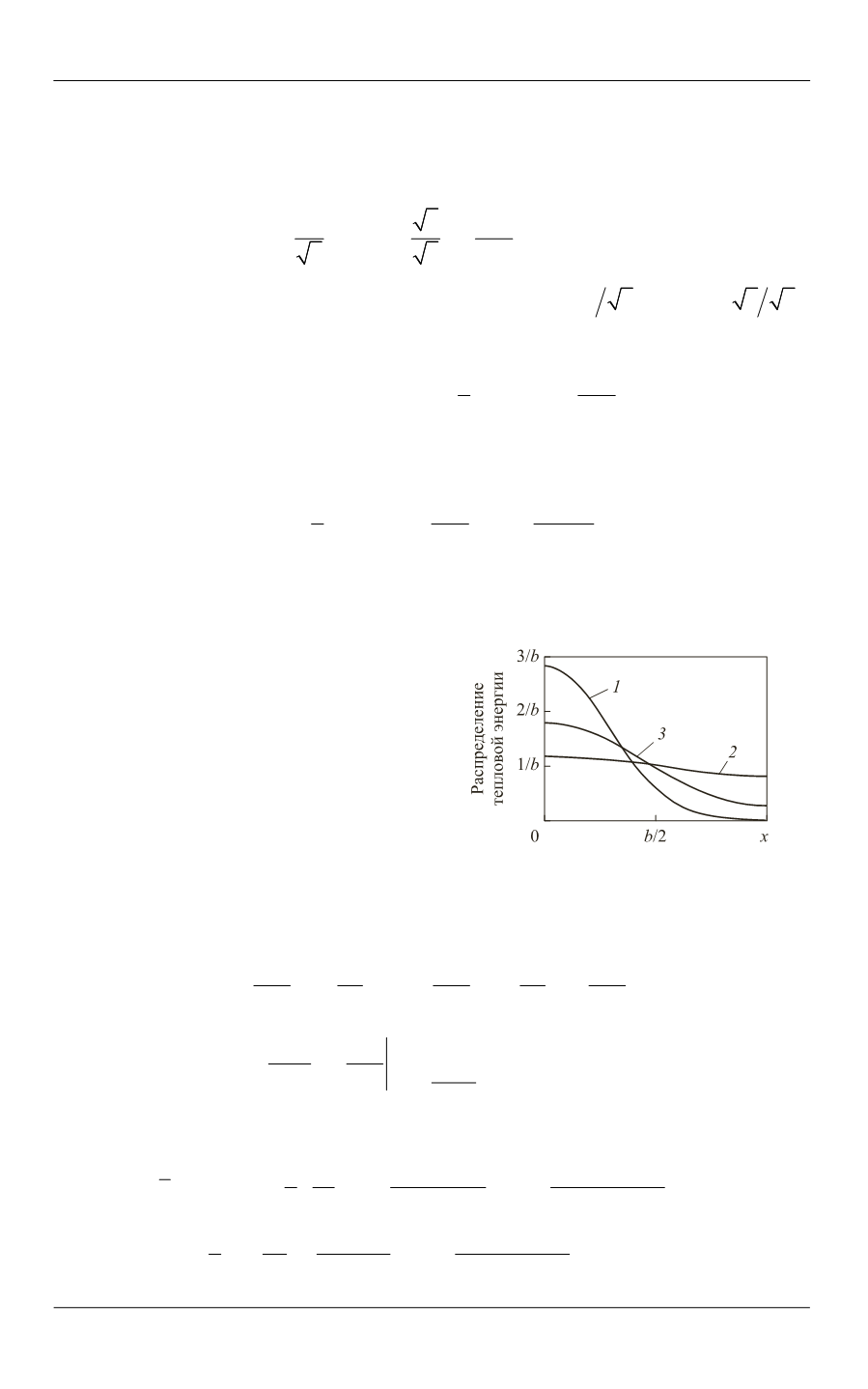
Распределение внутренней энергии при различных значениях времени
t
приведено на рис. 1.
Рис. 1.
Распределение внутренней энергии
при значениях времени
2
0,04 /
t
b a
(
1
),
2
0,25 /
t
b a
(
2
) и
2
0,1 /
t
b a
(
3
)
Найдем статический момент внутренней энергии. Для этого вычислим
вклад каждого слагаемого ряда Фурье:
0
0
0
2
2
2 2
0
2 2
cos
=
sin = 0
sin
=
0,
четно;
= cos
= 2 ,
нечетно.
b
b
b
b
nx
b
nx
b
nx
x
dx
xd
dx
b
n
b
n b
n
b
nx
b
n
b
n
n
Учитывая
=1
E
, получаем
2
2
2
2
2
2
2
=0
1
2
(2 1)
( ) = ( ) =
2
exp
=
2
(2 1)
x
k
b
b
k at
x t M t
b
k
b
2
2
2
2
2
=0
8
1
(2 1)
= 1
exp
= ( ),
2
(2 1)
k
b
k at
bX
k
b
(4)
















