
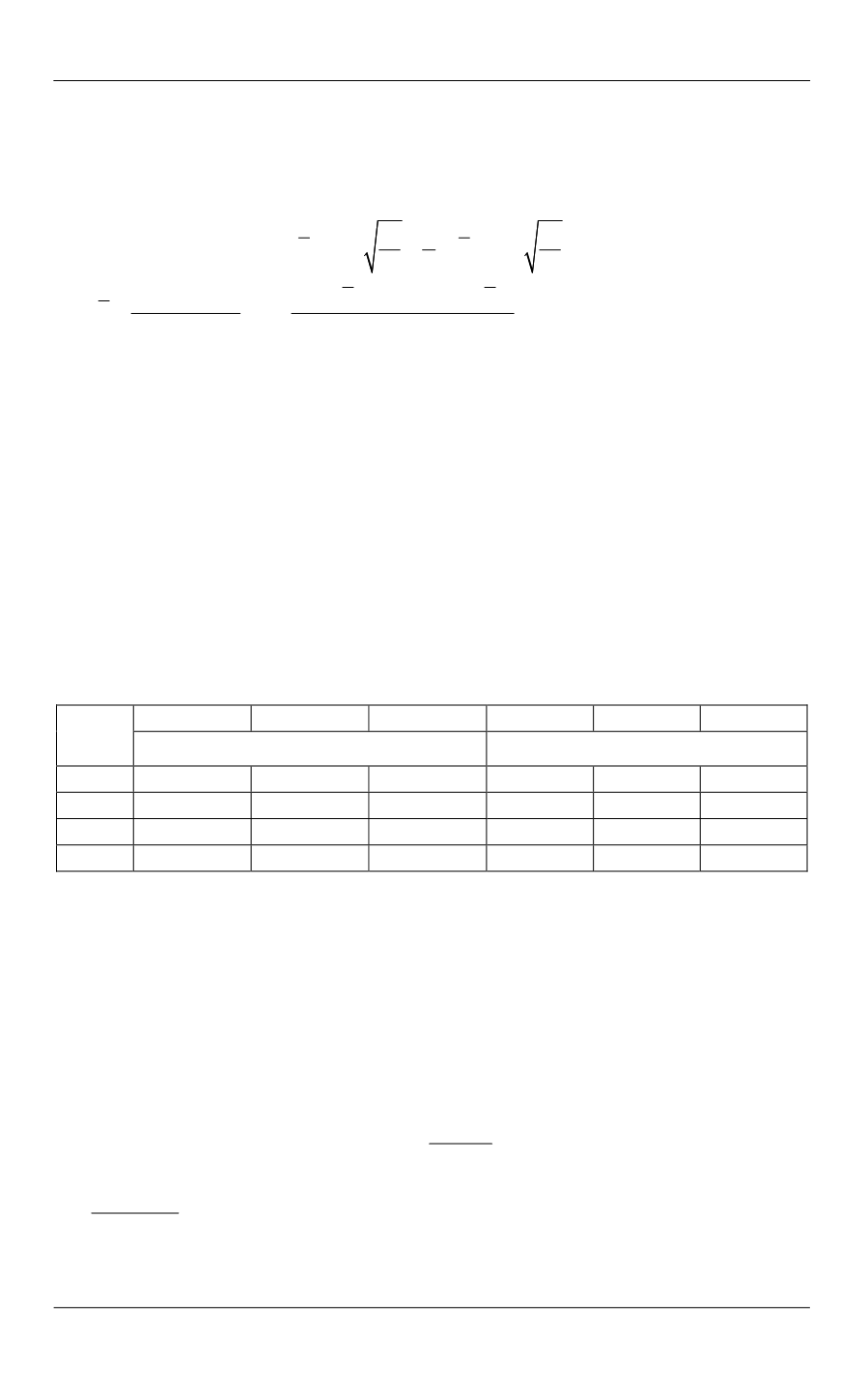
Нахождение эффективной теплопроводности композита методом моментов
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2016. № 4
35
ˆ /
a a
была апостериорно оценена по критерию Стьюдента. Разбив 4 300 частиц
на 10 серий по 430 частицы, вычислим оценки
ˆ /
a a
для каждой серии, обозна-
чив полученные значения через
1
, ,
A
10
.
A
Тогда 95%-ный доверительный ин-
тервал для оценок
ˆ /
a a
имеет вид
ˆ
2,26 < < 2,26 ,
10
10
S a
S
A
A
a
где
2
2
1
10
1
10
(
)
(
)
=
;
=
;
10
9
A A
A A
A A
A
S
число 2,26 — квантиль уров-
ня 0,975 распределения Стьюдента с девятью степенями свободы. К сожалению,
доверительные интервалы, вычисленные таким способом, не оказались более
узкими. Поэтому в дальнейших экспериментах было выбрано только значение
T
= 5 с.
Результаты, полученные для серий экспериментов, состоящих из = 4300
n
блуждающих частиц, с шагом времени
4
= 5 10 c,
t
при отношениях
/ =0,4
R D
и
2 1
/
= 0, 1/3, 1, 3 приведены в таблице. Полученные значения отношения
ˆ /
a a
с вероятностью 95 % имеют относительную погрешность менее 2 %. Слу-
чай
2 1
/ =1
(однородный материал), для которого известен точный ответ
ˆ / = 1,
a a
рассмотрен как тестовый.
Результаты, полученные для серий экспериментов с упорядоченными
и хаотическими шаровыми включениями,
/ = 0,4
R D
2 1
/
X
ˆ /
a a
ˆ /
X
ˆ /
a a
ˆ /
Упорядоченные шаровые включения
Хаотичные шаровые включения
0
0,2365
0,8794
0,6437
0,2394
0,9013
0,6597
1/3
0,2246
0,7928
0,7928
0,2269
0,8096
0,8096
1
0,2533
1,0101
1,0101
–
–
–
3
0,2928
1,3606
1,3606
0,2937
1,3694
1,3694
Пусть включения радиусом
< 0,5
R D
расположены хаотически с плотно-
стью
3
1/ .
D
Для каждой частицы задают в достаточно широком фрагменте слоя
случайное расположение включений, при этом не допускается их наложение
друг на друга и на начало координат, из которого частица начинает движение.
Результаты вычислительных экспериментов также представлены в таблице.
Сравним полученные результаты с результатами, полученными в работе [6],
в которой была выведена формула
1
1 2
ˆ / =
,
1
b
b
(6)
2 1
2 1
1 /
=
;
2 /
b
—
объемная концентрация включений. В рассматриваемом
случае
3
= 4 ( / ) / 3 0,268.
R D
















