
О.В. Пугачев, Зо Тун Хан
32
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2016. № 4
где
— безразмерная переменная,
2
= /
at b
;
( )
X
— безразмерная функция,
2
2
2
2
=0
1 8
1
( ) = 1
exp( (2 1) )
2
(2 1)
k
X
k
k
(рис. 2,
а
).
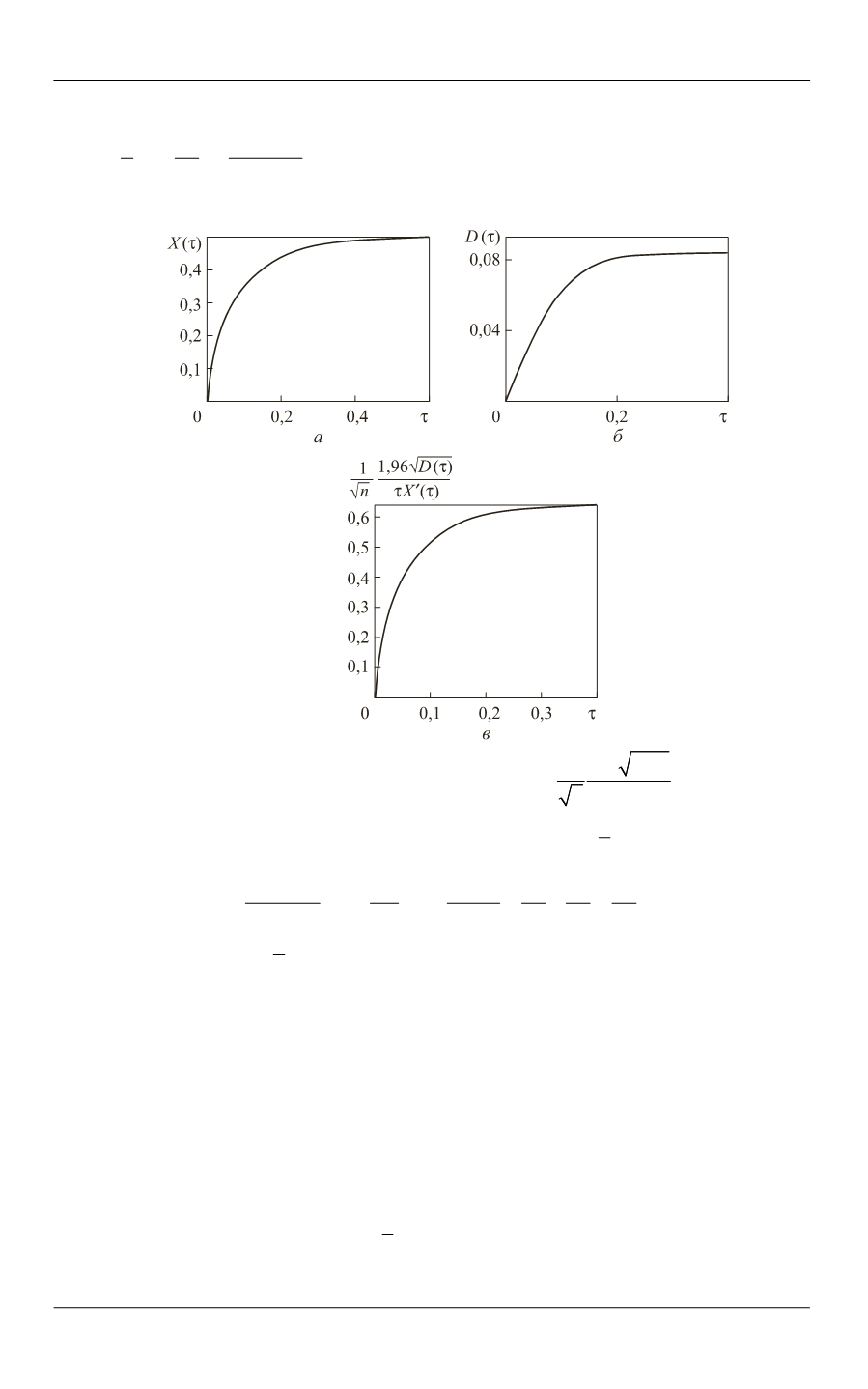
Рис. 2.
Графики функций
( )
X
(
а
),
( )
D
(
б
) и
1,96 ( )
1
( )
D
X n
(
в
)
Формула (4), как и следовало ожидать, при
= 0
t
дает
= 0,
x
так как
2
2
2
2
2
2
=0
=1
=1
1
1
1
=
=
= .
(2 1)
(2 )
6 24 8
k
m
m
k
m m
При
t
значение
( )
x t
стремится к
/ 2,
b
поскольку распределение внут-
ренней энергии сходится к равномерному.
Статистическая оценка центра внутренней энергии.
Пусть имеется слой
{0
}
x b
с теплоизолированными поверхностями, изготовленный из компози-
та с размерами неоднородностей, намного меньшими
,
b
эффективный коэффи-
циент температуропроводности
a
которого требуется найти. Проведем следую-
щий вычислительный эксперимент. Пусть
n
частиц стартуют с поверхности
{ = 0}
x
и совершают броуновское движение, описанное в работах [14, 15], отра-
жаясь от теплоизолированных поверхностей
{ = 0}
x
и
{ = }.
x b
В некоторый мо-
мент времени
t
вычислим среднее значение
ˆ ( )
x t
координаты
x
этих частиц. Его
математическое ожидание равно
( ).
x t
Определим дисперсию. Второй момент
внутренней энергии составляет
















