
Графовый подход при построении конечно-элементной модели упругих тел…
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 3
65
ных координат, описывающих разрезанное на элементы и связное тело. При
выводе определяющей системы уравнений важную роль играют вершинный и
контурный законы Кирхгофа для графов [16]. Этот подход подробно описан в
работах [4
–
6, 12]. Используемые при этом матрицы преобразований строятся
аналогично тому, как это сделано в работах [4, 9] для элементарной ячейки в
декартовой и цилиндрической системах координат.
Пример 1.
Рассмотрим задачу о напряженно-деформированном состоянии
тонкой двухслойной кольцевой пластины, находящейся под действием равно-
мерного давления на внутренней и внешней поверхности. Граничные условия
имеют вид:
1
rr
P
σ =
при
1
2
,
rr
r r
P
= σ = −
при
3 1
, ,
r r r
=
3
r
— внутренний и внеш-
ний радиусы. Упругие характеристики материала в пределах каждого слоя по-
стоянны. Условия сопряжения на границе концентрических колец при
2
r r
=
следующие:
( )
( )
1 2
2 2
,
r
r
r
r
σ = σ
( )
( )
1 2
2 2
.
r
r
u r u r
=
Здесь
(
)
1, 2
ri
i
σ =
— радиальная
компонента тензора напряжений в
i
-м слое;
ri
u
— перемещение
i
-го слоя в ра-
диальном направлении. Для этой задачи нетрудно получить точное аналитиче-
ское решение. Вследствие ограничения объема статьи оно не приведено. Для
анализа напряженного состояния в пластине выделена область
1
2
,
r r r
≤ ≤
0
45 ,
≤ ϕ ≤ °
которая покрывалась не очень плотной (28×16) сеткой элементар-
ных ячеек. В расчетах принято
r
1
= 7 мм,
r
2
= 14 мм,
r
3
= 21 мм,
Е
1
= 100 МПа,
E
2
=200 МПа,
P
1
=1 МПа,
P
2
= 0, ν
1
= ν
2
= 0,33.
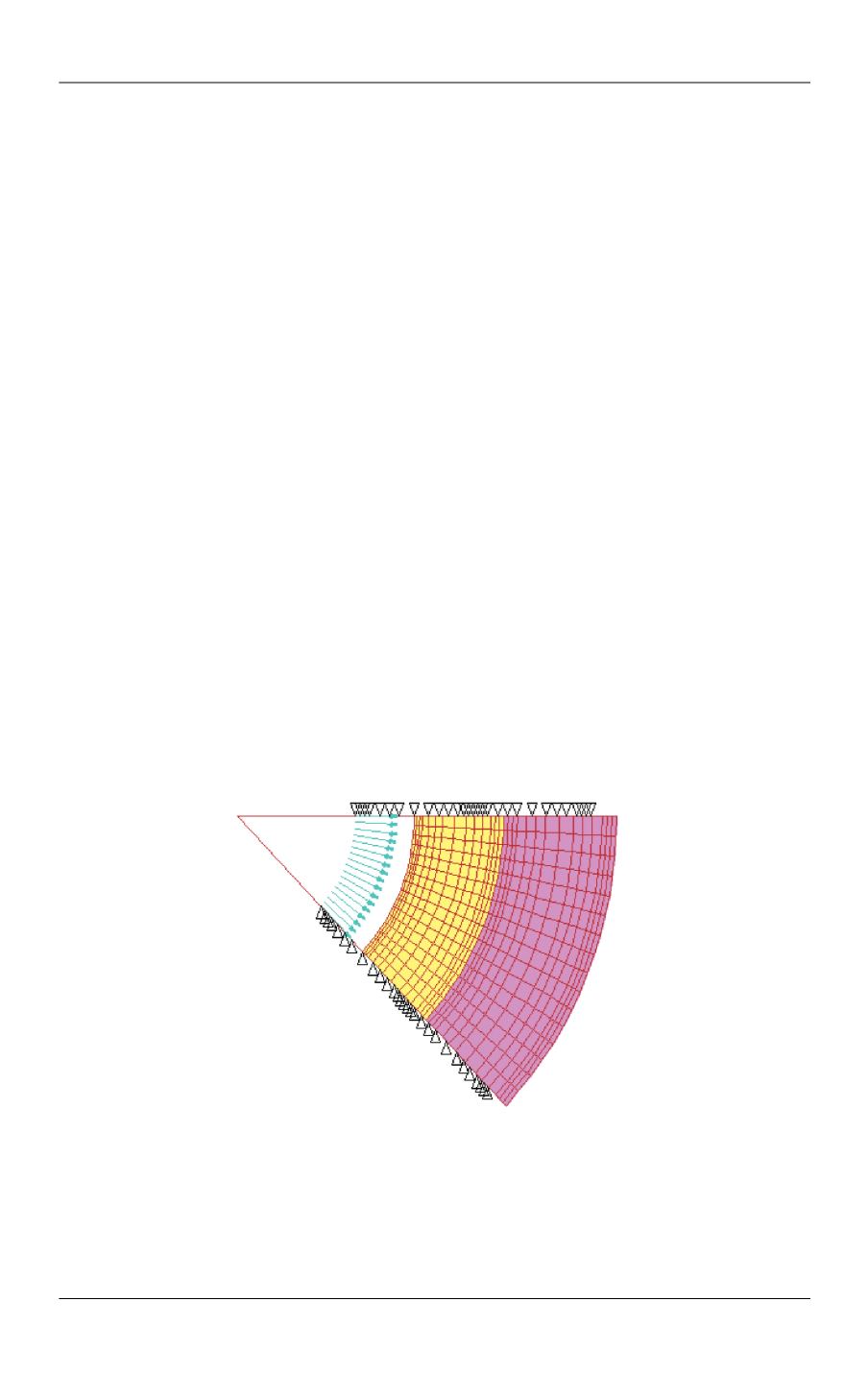
Вид двухслойной кольцевой пластины после деформирования представлен
на рис. 3. Стрелками показана равномерно распределенная нагрузка, причем
линия приложения нагрузки соответствует исходному недеформированному
состоянию пластины.
Рис. 3.
Вид двухслойной кольцевой пластины после деформирования
Значения радиальной компоненты тензора напряжений в зависимости от
радиуса
r
, полученные на основе графового метода, и соответствующее точное
аналитическое решение приведены в табл. 1. Полученные результаты хорошо
согласуются.
















