Графовый подход при построении конечно-элементной модели упругих тел в полярной системе координат

16 / 19

Графовый подход при построении конечно-элементной модели упругих тел…
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 3 67
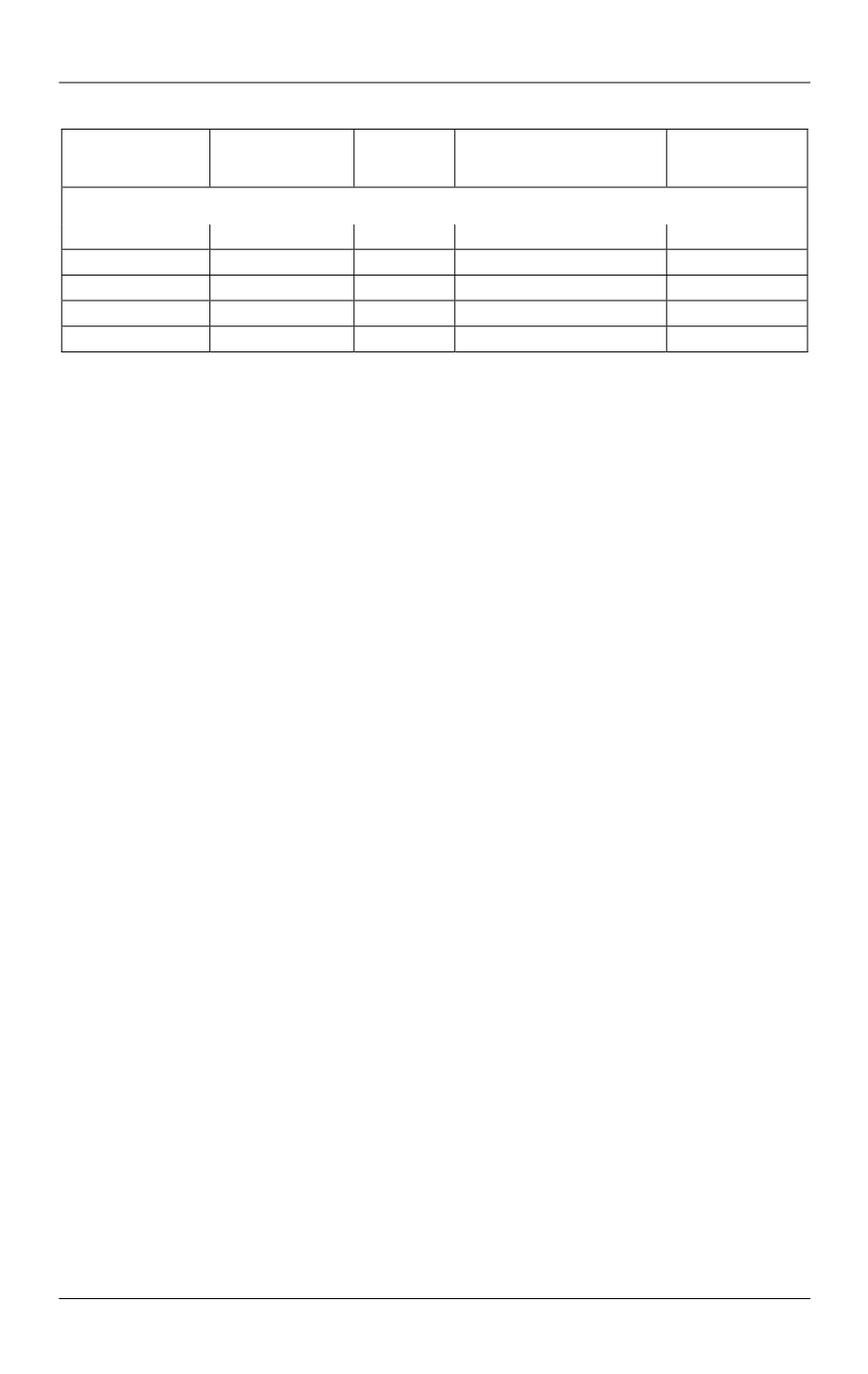
Окончание табл. 2
Тип элемента Число степеней
свободы
Число
элементов
Погрешность
определения радиально-
го смещения торца, %
Радиальное
смещение
торца, м
Регулярная форма элемента
QUAD8s 66 6 2,48 0,02380
QUAD91 78 6 1,99 0,02392
QUAD9t 78 6 1,42 0,02406
Графовый 28/42 6/12 3,15/0,84 0,02364/0,02420
Теоретический — — 0 0,02441
Заключение. Следует отметить, что при практическом применении числен-
ных методов важное значение имеет эффективность расчетной модели, под кото-
рой можно понимать достигаемую точность решения при фиксированном числе
степеней свободы. Поэтому число степеней свободы можно полагать некоторой
обобщенной характеристикой возможностей метода, определяющей в конечном
итоге вычислительные затраты.
Согласно данным, приведенным в табл. 2, графовый метод позволяет полу-
чить достаточно точные результаты на сетках с небольшим числом элементов и
при фиксированном числе степеней свободы превосходит по своим возможно-
стям стандартный МКЭ.
ЛИТЕРАТУРА
1. Trent H. Isomorphism between oriented linear graphs and lumped physical systems //
J. of the Acoustical Soc. of America. 1955. Vol. 27. No. 3. P. 500–527. DOI: 10.1121/1.1907949
URL:
2. Кузовков Е.Г. Конфигурация и параметры графовой модели упругого тела // Пробле-
мы прочности. 1986. № 4. С. 98–103.
3. Кузовков Е.Г. Уравнения состояния графовой модели упругого тела // Проблемы
прочности. 1986. №5. С. 112–117.
4. Кузовков Е.Г. Осесимметричная графовая модель упругого тела // Проблемы прочно-
сти. 1996. № 6. С. 83–103.
5. Кузовков Е.Г. Графовая модель упругой среды в декартовой системе координат //
Проблемы прочности. 1993. № 12. С. 60–70.
6. Тырымов А.А. Сингулярный элемент графовой модели упругой среды в декартовой
системе координат // Вычислительная механика сплошных сред. 2011. Т. 4. № 4. C. 125–
136. DOI: org/10.7242/1999-6691/2011.4.4.47
URL:
7. Тырымов А.А. Численное моделирование и расчет податливости образца с централь-
ной трещиной на основе графовой модели упругого тела // Труды МАИ. 2014. № 77.
URL:
8. Тырымов А.А. Численное решение осесимметричной задачи теории упругости на
основе графовой модели сплошной среды // Вестник Самарского гос. техн. ун-та. Серия:
Физико-математические науки. 2012. № 2. C. 103–114. DOI: 10.14498/vsgtu914
URL: