
А.А. Тырымов
66
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 3
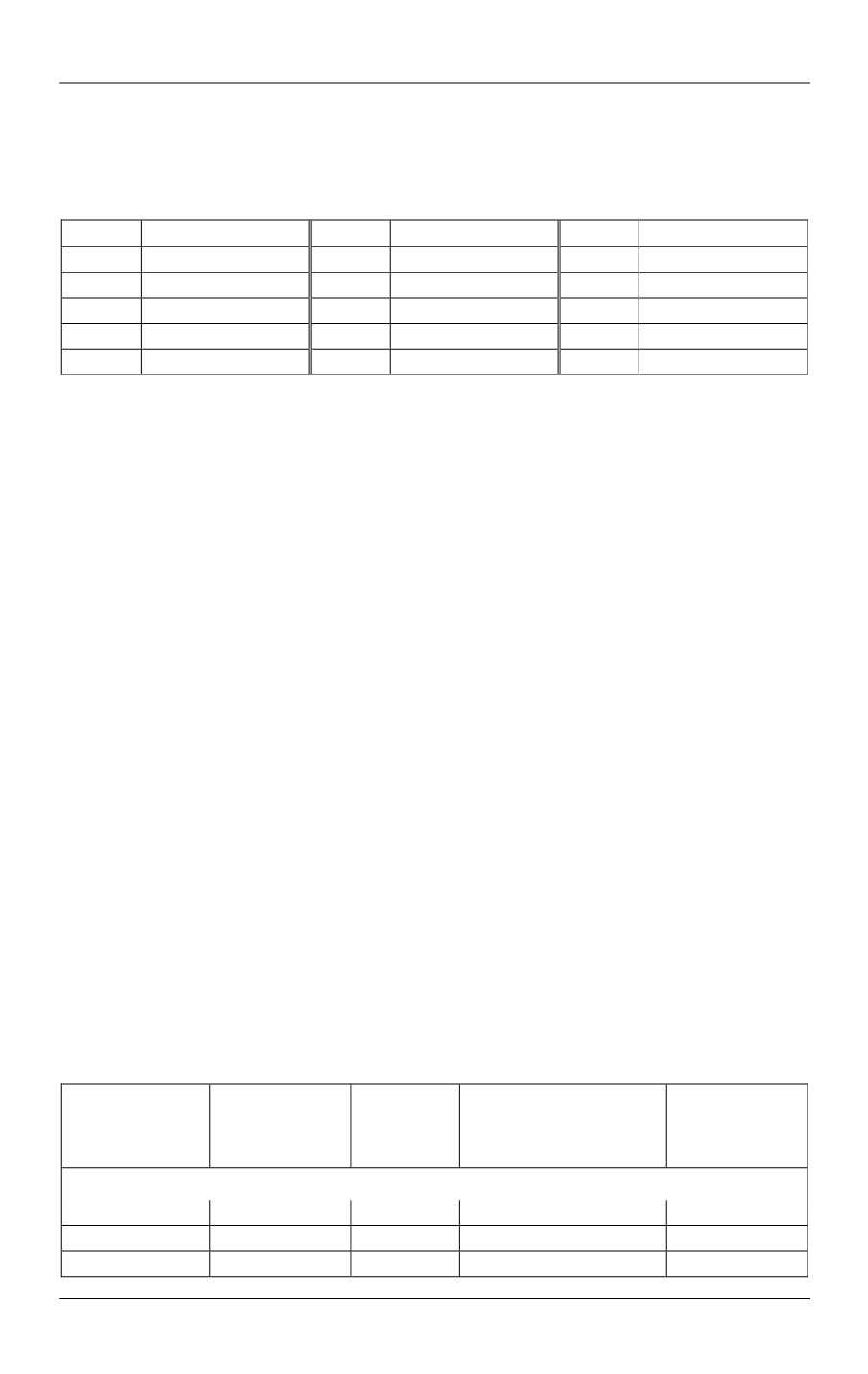
Таблица 1
Значения радиальной компоненты тензора напряжений в зависимости от радиуса
r
,
полученные на основе графового метода (числитель), и соответствующее точное ана-
литическое решение (знаменатель)
r
, мм
σ
r
/
P
r
, мм
σ
r
/
P
r
, мм
σ
r
/P
7
0,991/1,000
12
0,331/0,327
17
0,101/0,099
8
0,758/0,761
13
0,280/0,275
18
0,060/0,054
9
0,601/0,597
14
0,242/0,235
19
0,044/0,042
10
0,485/0,479
15
0,185/0,180
20
0,021/0,019
11
0,399/0,393
16
0,141/0,136
21
0,001/0,000
Пример 2.
Рассмотрим круговой брус узкого прямоугольного сечения, огра-
ниченный концентрическими окружностями радиусами
1 2 1 2
,
r r r r
и отрезка-
ми прямых
0,
/ 2
на его торцах. Дуги границы бруса свободны от
напряжений, один из торцов закреплен, а к другому — приложена сила
P
, дей-
ствующая в плоскости кольцевого сектора в радиальном направлении. Внешний
и внутренний радиусы бруса, а также упругие постоянные приняты такими же,
как и в работе [17]:
R
1
= 5,8661977 м;
R
2
= 6,8661977 м;
E
= 10
6
H/м
2
;
= 0,3;
P
= 10,0 H/м
2
.
Проанализируем радиальное перемещение незакрепленного торца стержня.
В работе [17] расчеты были проведены методом конечных элементов. Исполь-
зуются четырехугольный восьмиузловой серендиповский элемент (QUAD8s),
девятиузловой лагранжев элемент (QUAD91) и девятиузловой элемент, состав-
ленный из двух шестиузловых треугольных элементов. Показано, что геометри-
ческие формы элемента существенно влияют на точность результатов расчетов.
При использовании формы элементов, соответствующих регулярному разбие-
нию области в радиальном и окружном направлениях (именно такая сетка в
графовом методе), точность значительно выше, чем при криволинейных асим-
метричных очертаниях элементов.
Сравнение результатов расчетов значений радиального перемещения свобод-
ного конца стержня, полученных на основе графового метода и в работе [17], при-
ведено в табл. 2.
Таблица 2
Результаты расчетов значений радиального перемещения свободного конца
стержня, полученные на основе графового метода и в работе [17]
Тип элемента
Число степеней
свободы
Число
элементов
Погрешность
определения радиаль-
ного смещения торца, %
Радиальное
смещение
торца, м
Криволинейная форма элемента
QUAD8s
66
6
22,56
0,01890
QUAD91
78
6
15,39
0,02065
QUAD9t
78
6
3,14
0,02364
















