
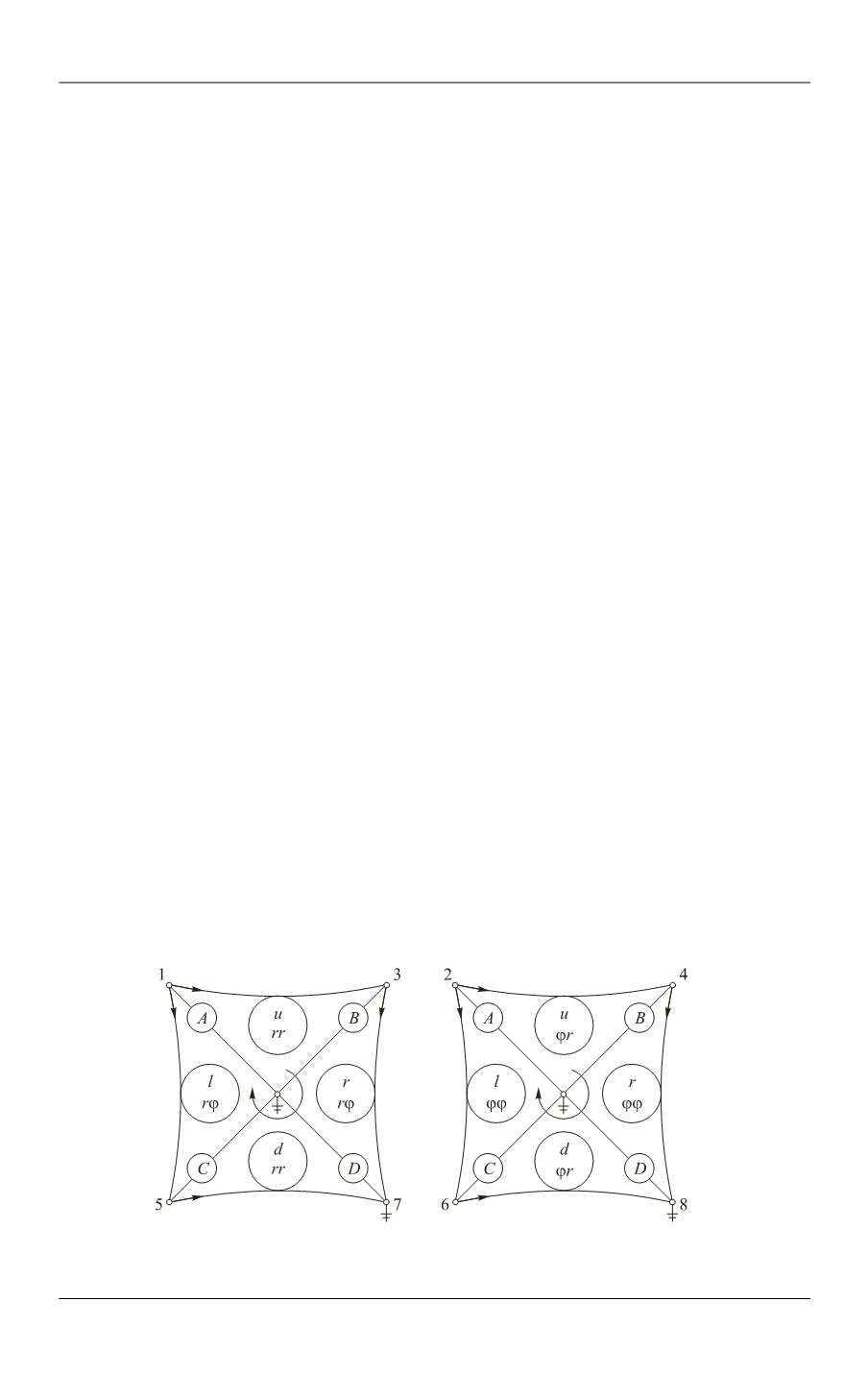
Графовый подход при построении конечно-элементной модели упругих тел…
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 3
55
будем называть подграф, соответствующий одному элементу, который получен
при разбиении исходной области на отдельные части.
При построении конфигурации элементарной ячейки в полярной системе
координат тело покрываем сетью координатных линий
=
ϕ =
const,
const,
r
между узлами которых устанавливаем гипотетические измерители. Здесь подра-
зумеваются идеализированные приборы, т. е. приборы, обладающие необходи-
мой базой, возможностью устанавливать ножки разных приборов в одну и ту
же точку среды. Полученную сеть измерителей преобразовываем в граф, пред-
ставляя каждый прибор дугой, а узлы, между которыми осуществлялось изме-
рение, — вершинами графа. При этом учитываем, что одна и та же геометриче-
ская точка среды, связанная с различными группами измерений, должна быть
представлена разными вершинами.
Если вершины элемента обозначить через
A, B, C
и
D
, то измерители необ-
ходимо установить так, чтобы измерять перемещения точек
A, B, C
и
D
относи-
тельно друг друга (деформации
ϕ ϕϕ ϕ
δ δ δ δ
,
,
,
rr r
r
) и относительно системы коор-
динат (перемещения
ϕ ϕ ϕ ϕ
,
,
,
,
,
,
,
A B C D A B C D
r
r
r
r
u u u u u u u u
). Например, деформация
δ
rr
измеряется между точками
А
и
B
, либо
C
и
D
оси
r
, деформация
ϕ
δ
r
— меж-
ду точками
А
и
С
, либо
В
и
D
оси
ϕ
; деформация
ϕϕ
δ
— между точками
А
и
С
,
либо
В
и
D
оси
ϕ
, а деформация
ϕ
δ
r
— между точками
А
и
B
, либо
C
и
D
оси
r
.
Символ перемещения, для измерения которого был использован прибор, свя-
зываем с каждой дугой. Расположение дуг, отображающих измерения нормаль-
ных деформаций
ϕϕ
δ δ
( ,
),
rr
совпадают по направлению с этими деформациями.
Дуги, представляющие собой замеры относительных смещений
ϕ ϕ
δ δ
( ,
),
r
r
вы-
званных поворотом сторон элемента, расположены перпендикулярно соответ-
ствующим перемещениям. Ориентация дуг, как и ориентация процесса измере-
ния, совпадает с направлением осей координат.
В соответствии с описанной процедурой получаем элементарную ячейку че-
тырехугольного элемента в полярной системе координат, состоящую из двух
компонент (рис. 1). Дуговые стрелки в центре показывают направление обхода
контура.
Рис. 1.
Элементарная ячейка четырехугольного элемента в полярной системе
координат, состоящая из двух компонент
















