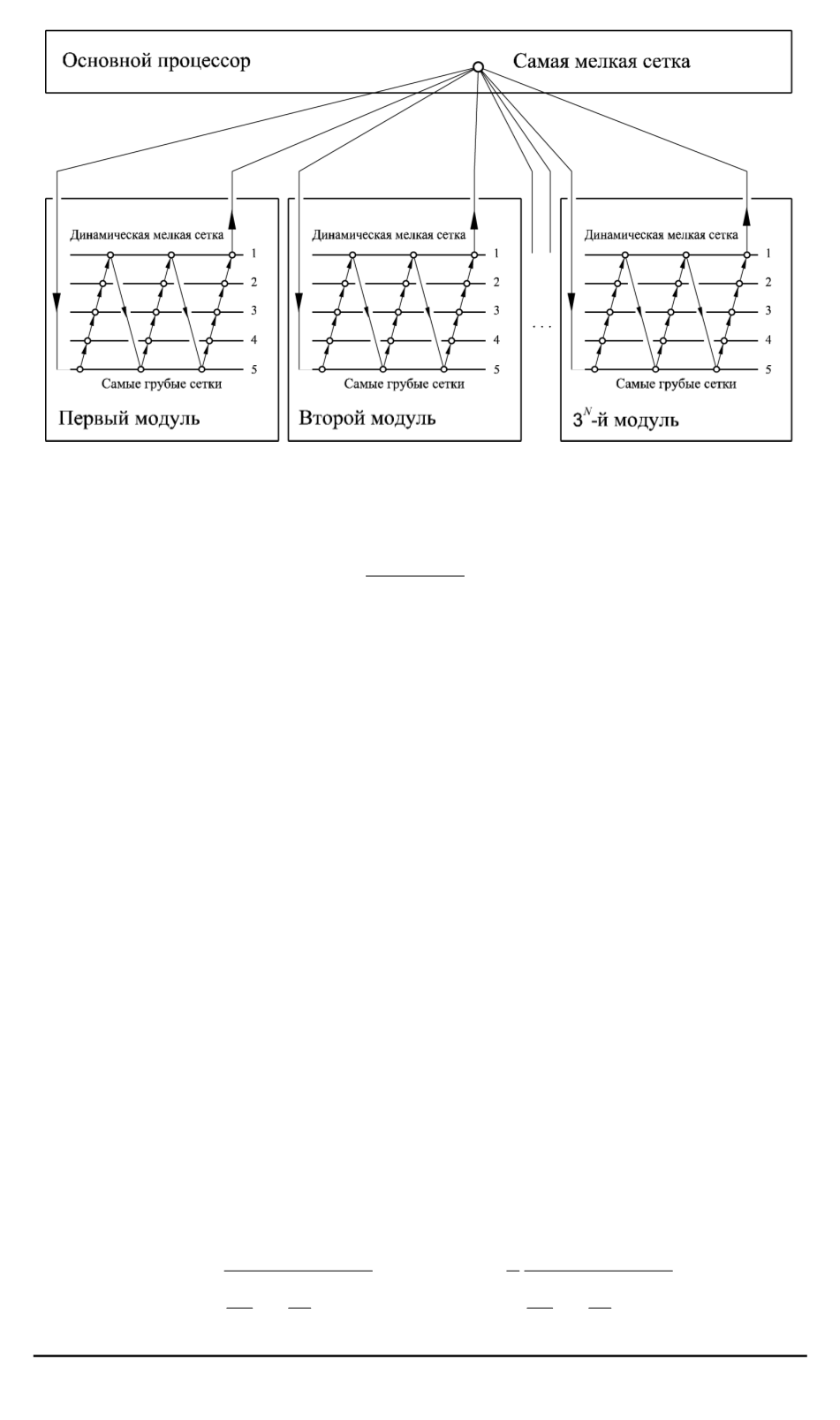
Рис. 7. Частичное распараллеливание УМТ (динамический цикл с
q
= 3
)
Тогда оценка (6) принимает вид
S
min
=
p
q L
+
+ 1
q L
+
+
p
=
pE
min
.
(7)
Значения минимальных ускорения (
S
min
) и эффективности паралле-
лизма (
E
min
) при решении двумерных (
N
= 2
) и трехмерных (
N
= 3
)
задач приведены в табл. 2. Очевидно, что эффективность распарал-
леливания динамического цикла (
q >
1
) выше, чем статического
(
q
= 1
) из-за перераспределения вычислительных усилий в пользу
уровней с грубыми сетками, где УМТ обладает полным параллелиз-
мом.
Полное распараллеливание УМТ.
Из оценки (7) также следует,
что эффективность распараллеливания УМТ сильно зависит от эф-
фективности распараллеливания сглаживающих итераций на самой
мелкой сетке. Сначала рассмотрим распараллеливание первой глуби-
ны при тех же допущениях (на каждой сетке выполняется одинаковое
число одних и тех же сглаживающих итераций).
Первая глубина.
Предположим, что на самой мелкой сетке (нуле-
вой сеточный уровень
l
= 0
) удалось некоторым образом распарал-
лелить сглаживающие итерации с ускорением
S
0
и эффективностью
E
0
. Тогда, согласно определению (2), время выполнения сглаживаю-
щих итераций на самой мелкой сетке составит
T
0
/S
0
. В данном случае
выражения (4) принимают вид
S
Σ
=
T
0
+
q
L
+
P
l
=1
T
l
T
0
S
0
+
q
p
L
+
P
l
=1
T
l
;
E
Σ
=
1
p
T
0
+
q
L
+
P
l
=1
T
l
T
0
S
0
+
q
p
L
+
P
l
=1
T
l
,
(8)
72
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 4


