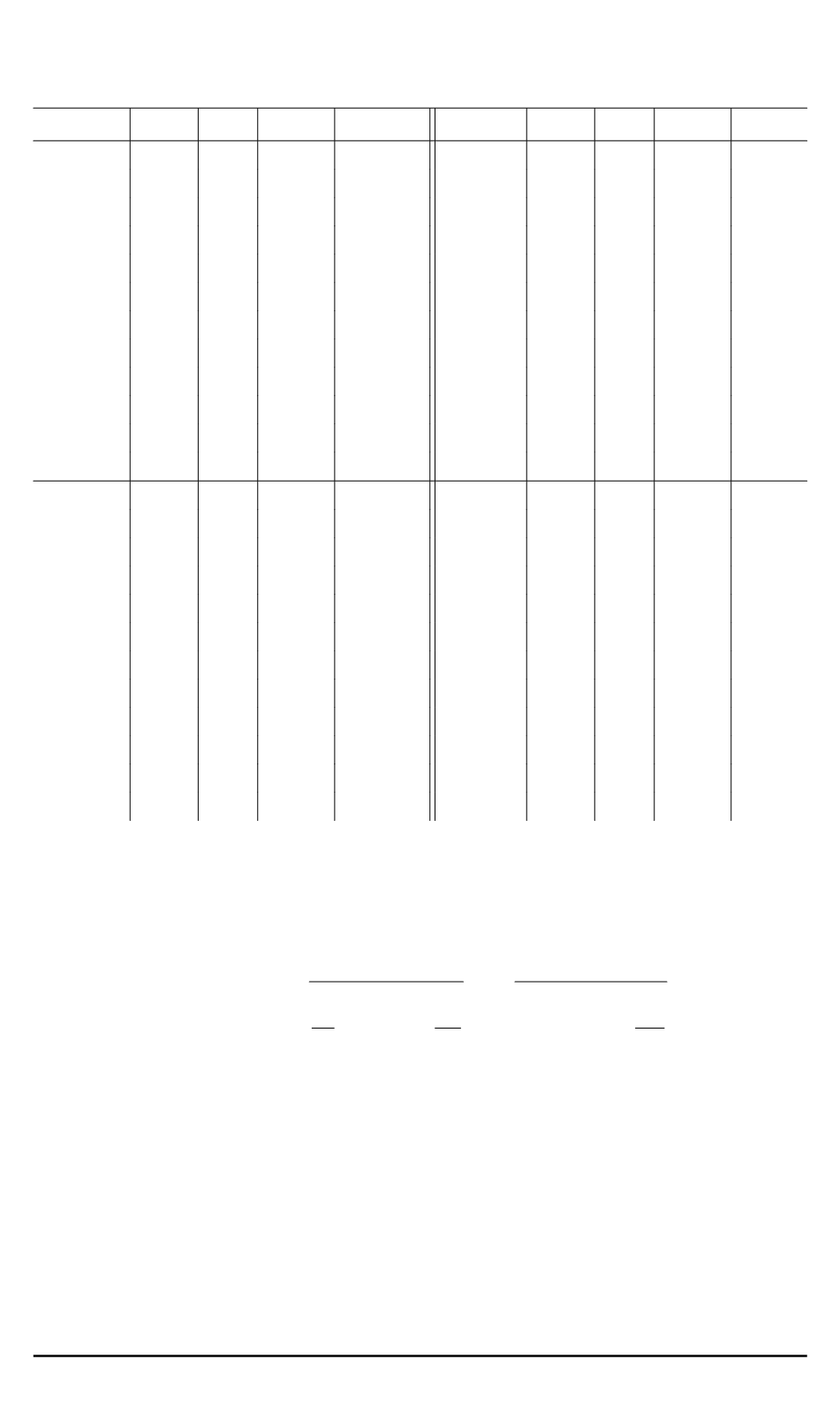
Таблица 3
Значения ускорения и эффективности параллелизма при решении
трехмерных задач на 27 процессорах
E
0
б %
L
+
q
S
Σ
E
Σ
, %
E
0
, %
L
+
q
S
Σ
E
Σ
, %
60,0
5 1 24,3 90,0
70,0
5 1 25,2 93,3
60,0
5 2 25,5 94,3
70,0
5 2 26,0 96,3
60,0
5 3 25,9 96,0
70,0
5 3 26,3 97,4
60,0
5 4 26,2 96,9
70,0
5 4 26,5 98,0
60,0
6 1 24,7 91,3
70,0
6 1 25,4 94,2
60,0
6 2 25,7 95,1
70,0
6 2 26,1 96,8
60,0
6 3 26,1 96,6
70,0
6 3 26,4 97,8
60,0
6 4 26,3 97,4
70,0
6 4 26,5 98,3
60,0
7 1 24,9 92,3
70,0
7 1 25,6 94,9
60,0
7 2 25,9 95,7
70,0
7 2 26,2 97,2
60,0
7 3 26,2 97,1
70,0
7 3 26,5 98,1
60,0
7 4 26,4 97,8
70,0
7 4 26,6 98,5
80,0
5 1 25,9 96,0
90,0
5 1 26,5 98,2
80,0
5 2 26,4 97,8
90,0
5 2 26,7 99,0
80,0
5 3 26,6 98,5
90,0
5 3 26,8 99,3
80,0
5 4 26,7 98,8
90,0
5 4 26,9 99,5
80,0
6 1 26,1 96,6
90,0
6 1 26,6 98,4
80,0
6 2 26,5 98,1
90,0
6 2 26,8 99,2
80,0
6 3 26,6 98,7
90,0
6 3 26,8 99,4
80,0
6 4 26,7 99,0
90,0
6 4 26,9 99,6
80,0
7 1 26,2 97,0
90,0
7 1 26,6 98,6
80,0
7 2 26,6 98,4
90,0
7 2 26,8 99,3
80,0
7 3 26,7 98,9
90,0
7 3 26,9 99,5
80,0
7 4 26,8 99,2
90,0
7 4 26,9 99,6
случае принимает вид
S
Σ
=
pE
Σ
=
q
L
+
X
l
=1
ν
l
+
ν
0
q
p
L
+
X
l
=1
ν
l
+
ν
0
S
0
=
p
q
L
+
X
l
=1
ν
l
+
ν
0
q
L
+
X
l
=1
ν
l
+
ν
0
E
0
.
(10)
Увеличение числа сглаживающих итераций на самой мелкой сетке
(
ν
0
> ν
l
)
приведет к незначительному уменьшению эффективности
параллелизма.
Вторая глубина или массивное распараллеливание.
Современ-
ная многопроцессорная техника позволяет использовать сотни и даже
тысячи процессоров для распараллеливания вычислений. Рассмотрим
распараллеливание второй глубины при решении трехмерных задач,
т.е. число используемых процессоров составит
p
= 3
6
= 729
. Предпо-
74
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 4


