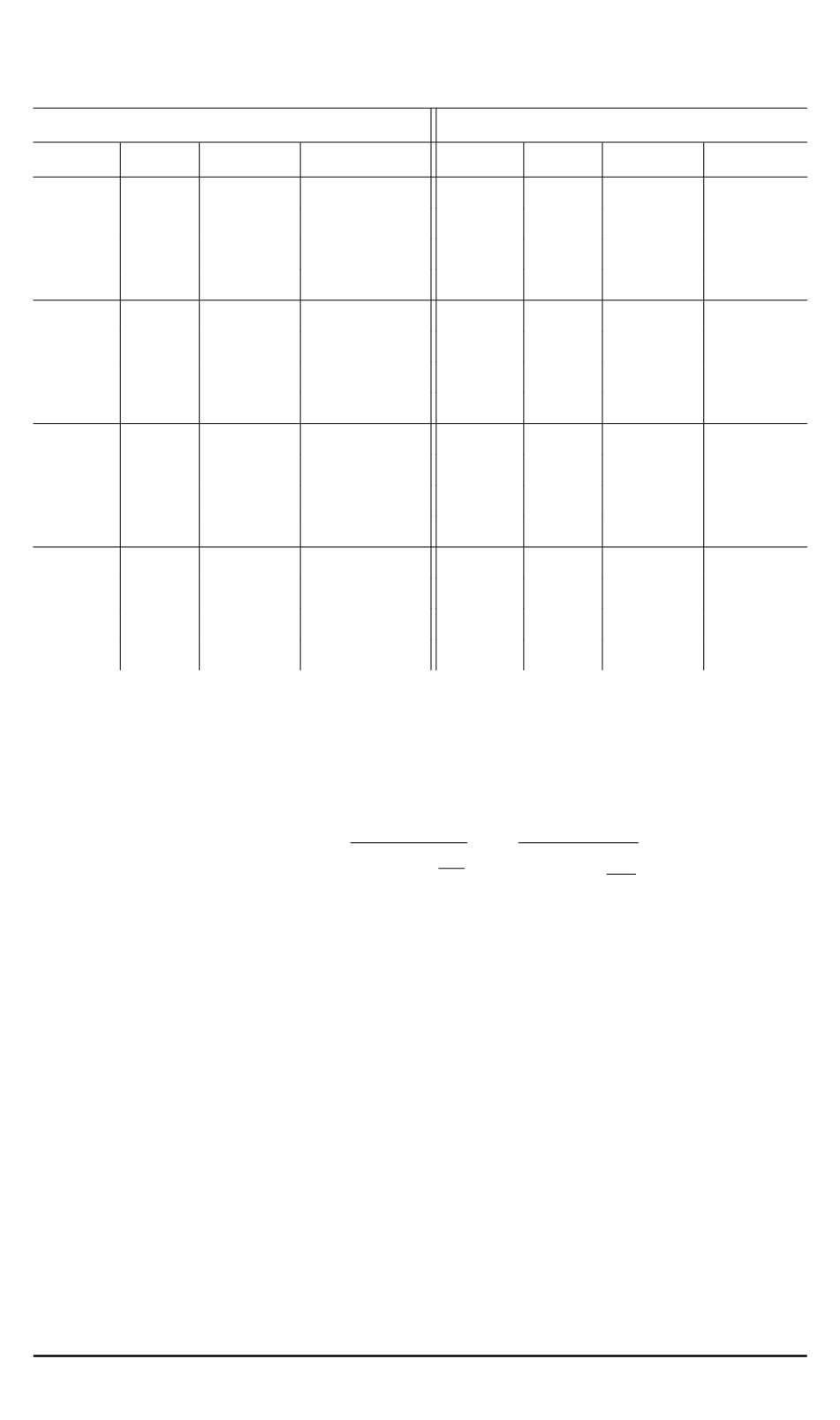
Таблица 2
Значения минимальных ускорения и эффективности параллелизма при
решении двумерных и трехмерных задач
N
= 2
(
p
= 9
)
N
= 3
(
p
= 27
)
L
+
q
S
min
E
min
, %
L
+
q
S
min
E
min
, %
4
1
3,5
38,4
4
1
4,4
16,1
4
2
4,8
52,9
4
2
6,9
25,7
4
3
5,6
61,9
4
3
9,0
33,3
4
4
6,1
68,0
4
4
10,7
39,5
5
1
3,9
42,9
5
1
5,1
18,8
5
2
5,2
57,9
5
2
8,0
29,7
5
3
6,0
66,7
5
3
10,3
38,1
5
4
6,5
72,4
5
4
12,1
44,7
6
1
4,2
46,7
6
1
5,7
21,2
6
2
5,6
61,9
6
2
9,0
33,3
6
3
6,3
70,4
6
3
11,4
42,2
6
4
6,8
75,8
6
4
13,2
49,0
7
1
4,5
50,4
7
1
6,4
23,5
7
2
5,9
65,9
7
2
9,9
36,6
7
3
6,6
73,9
7
3
12,4
45,8
7
4
7,0
78,0
7
4
14,2
52,7
где
S
Σ
и
E
Σ
— ускорение и эффективность параллельного исполнения
УМТ. Отметим, что
S
min
0
= 1
и
E
min
0
= 1
/p
.
Тогда в силу допущения
T
l
=
const выражения (8) принимают вид
S
Σ
=
pE
Σ
=
p
q L
+
+ 1
q L
+
+
p
S
0
=
p
q L
+
+ 1
q L
+
+
1
E
0
.
(9)
В табл. 3 приведены значения ускорения и эффективности парал-
лелизма при решении трехмерных задач (
N
= 3
, p
= 3
N
= 27
). Полу-
ченное значение эффективности
E
Σ
оказалось не ниже
90
% даже при
использовании статического цикла (
q
= 1
).
В работе [11] показано, что сглаживание на уровнях с более мел-
кими сетками оказывает б´ольшее влияние на скорость сходимости
УМТ, чем сглаживание на уровнях с более грубыми сетками. Поэтому
при решении прикладных задач возможен случай, когда на различ-
ных уровнях
l
выполняется разное число сглаживающих итераций
ν
l
.
В этом случае время, необходимое для выполнения сглаживающих
итераций на сетках уровня
l
, составит
T
l
=
αν
l
, где
α
есть некий
коэффициент пропорциональности, зависящий от сглаживающей про-
цедуры. Оценка ускорения и эффективности параллелизма в данном
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 4
73


