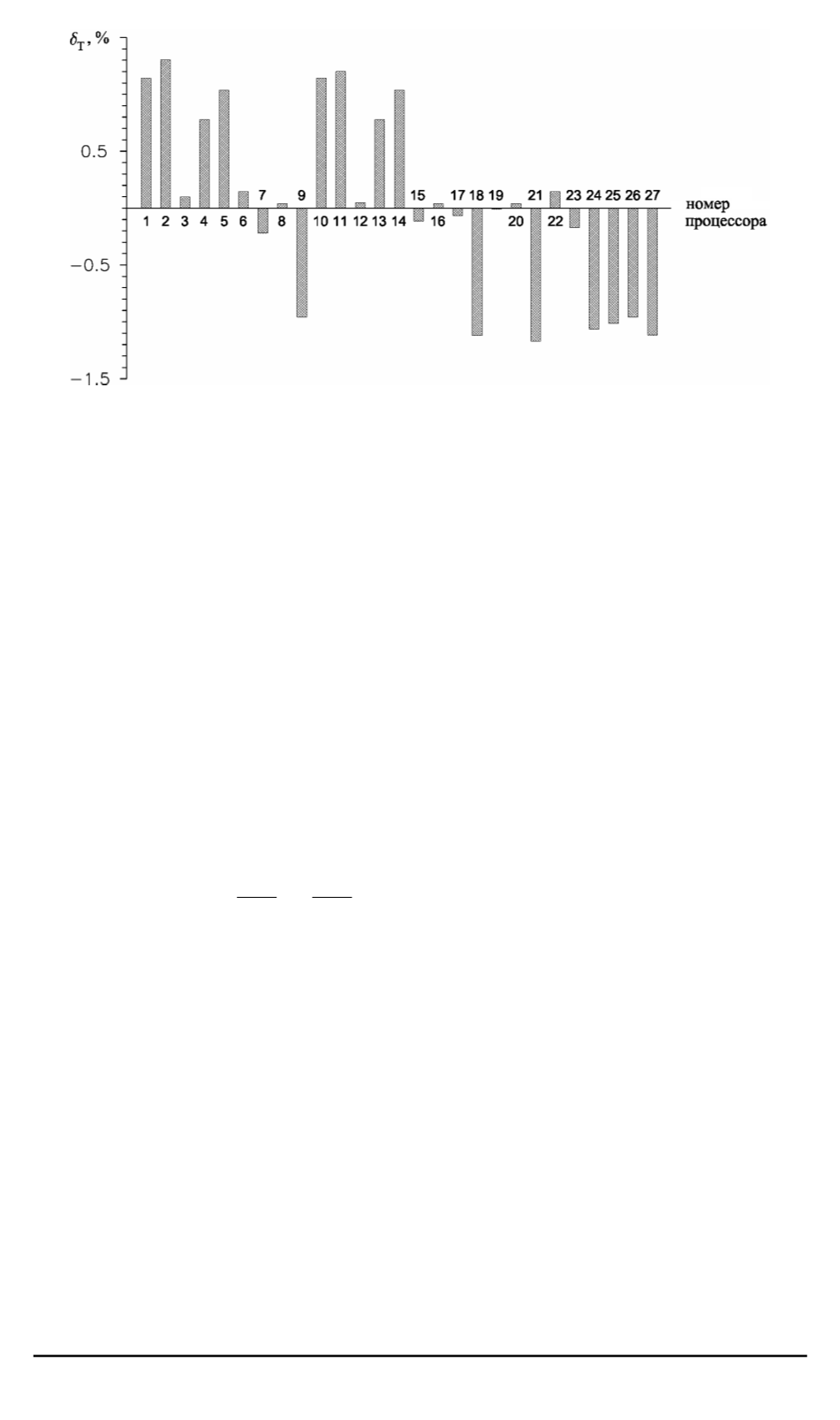
Рис. 6. Отклонение времени выполнения сглаживающих итераций предобу-
словленного метода сопряженных градиентов от среднего значения на сетках
первого уровня и их подсетках
Результаты вычислительного эксперимента, приведенные на рис. 6,
показывают, что максимальное отклонение времени выполнения сгла-
живающих итераций предобусловленного метода сопряженных гра-
диентов на
i
-м процессоре от среднего значения
h
T
i
не превышает
одного процента. Другими словами, сглаживающая процедура на сет-
ках первого уровня и их подсетках состоит из
3
N
независимых задач,
решение которых требует почти одинакового времени. Тем самым до-
стигается почти равномерная загрузка процессоров.
Следующий вычислительный эксперимент посвящен проверке до-
пущения об одинаковом времени выполнения сглаживающих итера-
ций на различных сеточных уровнях (т.е.
T
l
=
const). Для этого рас-
смотрим первую краевую задачу для уравнения
∂
2
u
∂x
2
+
∂
2
u
∂y
2
=
−
f
(
x, y, z
) = 2
e
x
−
y
,
в единичном квадрате, которая имеет точное решение
u
a
(
x, y
) =
e
x
−
y
,
откуда нетрудно найти соответствующие граничные условия. Числен-
ное решение данной задачи проведем на семиуровневой многосеточ-
ной структуре (
L
+
= 6
) с самой мелкой сеткой
2001
×
2001
, начиная с
нулевого начального приближения. В качестве сглаживающей проце-
дуры использован метод Зейделя с точечным упорядочиванием неиз-
вестных. Полное время выполнения многосеточной итерации принято
за
100
%.
В табл. 1 показано распределение относительного времени счета
по сеточным уровням
T
l
.
L
+
+1
X
l
=0
T
l
и уменьшение ошибки численного
70
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 4


