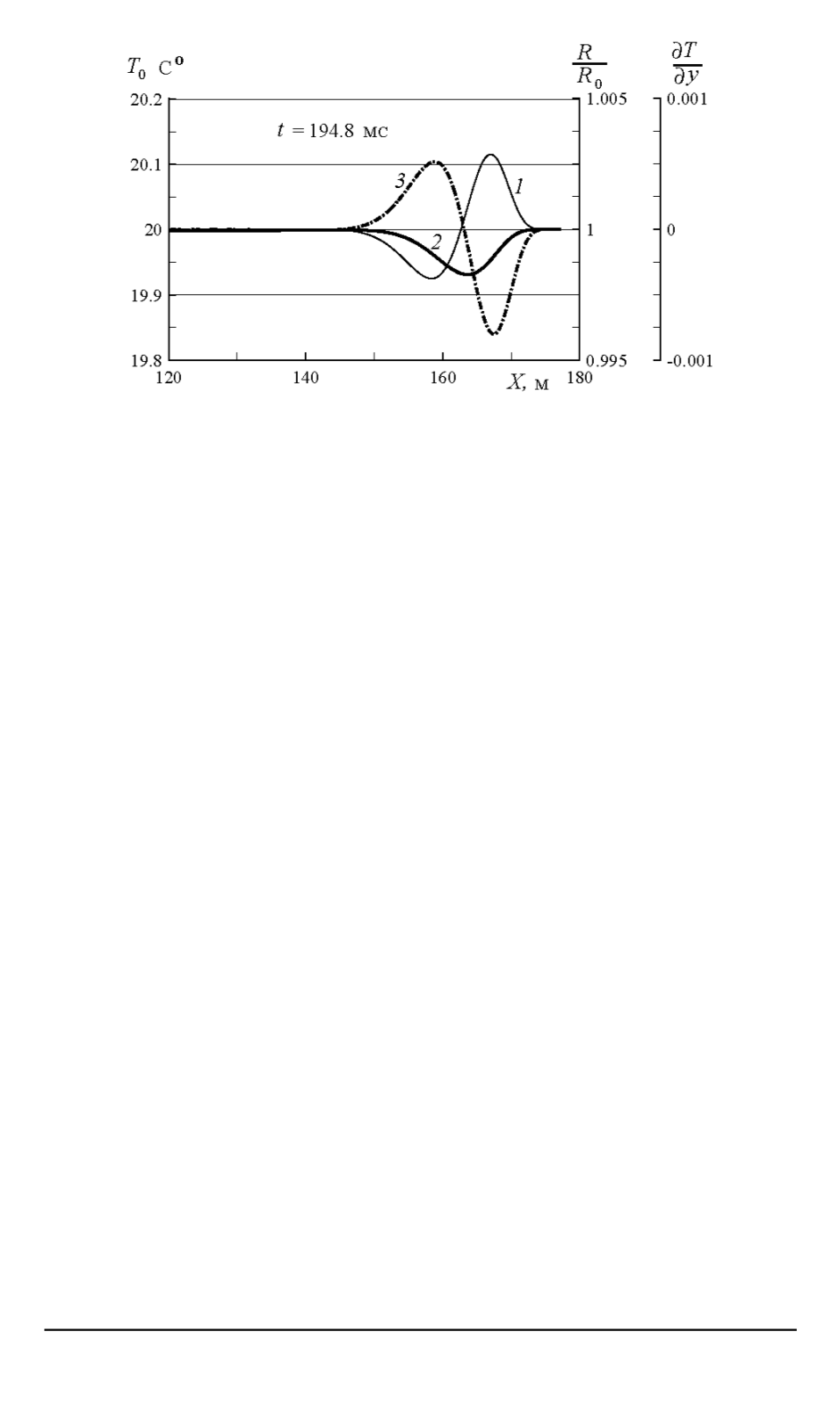
Рис. 6. Пространственные профили температуры
T
0
(
1
), радиуса пузырьков
R
(
2
) и безразмерного градиента температуры
(
∂T/∂y
)
|
y
=1
(
3
)
принять политропический закон поведения газа, так как в этом слу-
чае любому состоянию с меньшим радиусом должна соответствовать
б´ольшая температура
T
0
> T
L
, а в изотермическом случае
T
0
=
T
L
.
Волнообразное поведение
T
0
возможно только при немонотонном тем-
пературном профиле внутри пузырьков. Обратим внимание на то, что
процесс очень медленный, но поведение газа не изотермическое, его
температура не постоянна и не равна
T
L
вопреки интуитивно приня-
тому представлению для низкочастотного приближения во всех лите-
ратурных источниках.
Соответственно, в первой подобласти (т.е. на переднем фронте
волны сжатия) температура центров выше температуры окружающей
жидкости, а во второй подобласти (на заднем фронте волны сжа-
тия) температура центров ниже температуры окружающей жидкости.
В первой полуволне у пузырьков градиент температуры на стенке
(кривая
3
на рис. 6) отрицателен и все пузырьки этого гребня отдают
теплоту в жидкость, а во второй полуволне градиент температуры по-
ложителен и все пузырьки, попавшие в этот второй гребень, получают
теплоту из жидкости.
Было проведено также моделирование с другими частотами и ам-
плитудами возбуждающего акустического возмущения. Качественно
картина эволюции акустической волны осталась прежней. В результа-
те выявлено, что уменьшение только одного параметра частоты в два
раза (
ω
=
ω
0
/
40
) при неизменных прочих параметрах задачи привело
к росту амплитуды уединенной волны почти вдвое. Данный резуль-
тат можно объяснить с позиций второго начала термодинамики. Чем
медленнее происходит цикл сжатия и расширения пузырька, тем он
ближе к обратимому процессу, а значит, тем меньше потери энергии
на первом и втором этапах формирования уединенной волны.
20
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 1


