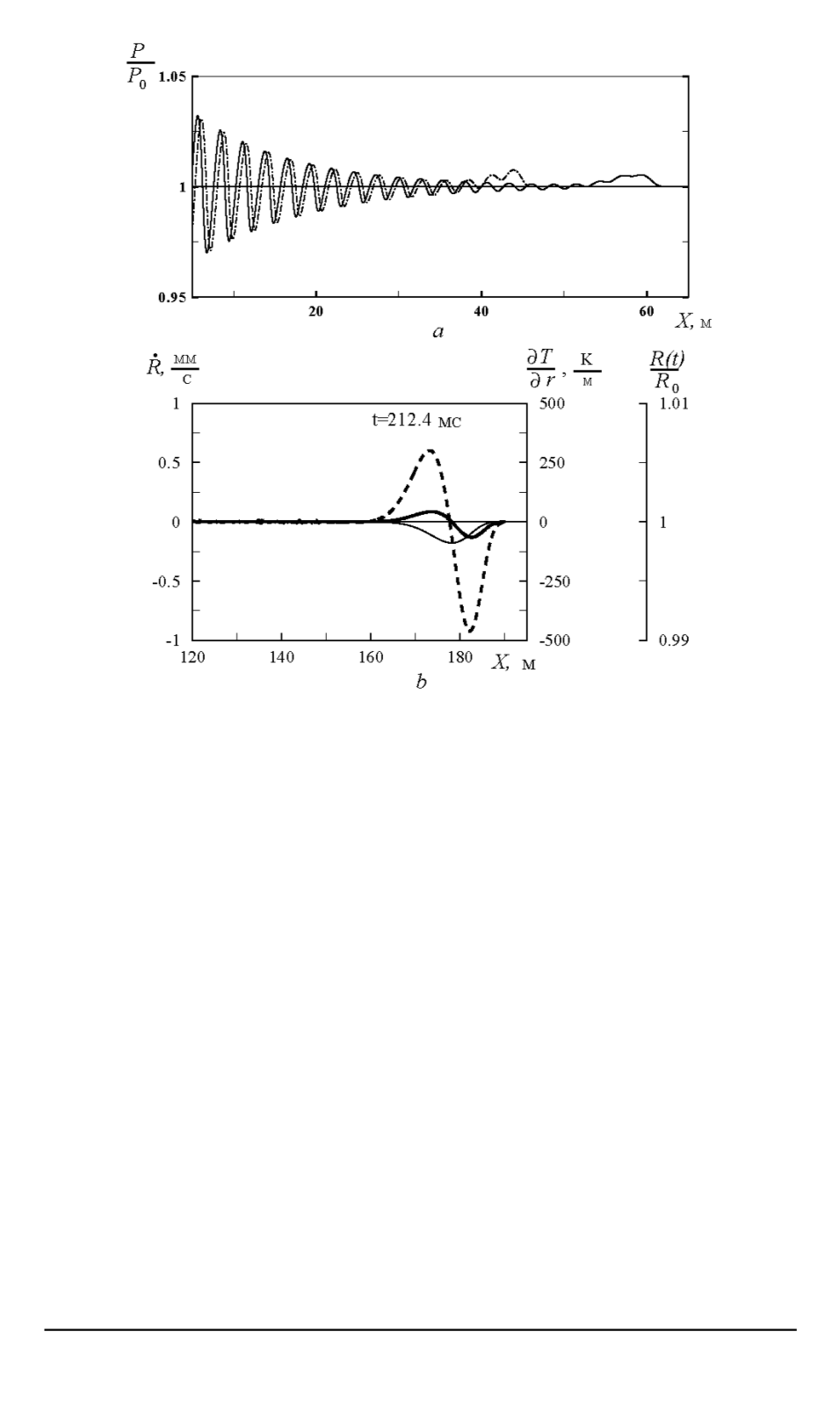
Рис. 4. Первый, второй (
a
) и третий (
b
) этапы эволюции исходной звуковой вол-
ны в нелинейной, диспергируюшей и диссипативной газожидкостной системе
третьим гребнем, как показано на сплошной кривой в момент време-
ни
t
= 68
,
5
мс. В результате к моменту времени
t
= 110
мс образуется
предельная конфигурация — стационарная уединенная волна.
Уединенная волна радиусов показана на рис. 4,
б
в момент време-
ни
t
= 212
,
4
мс (тонкая сплошная кривая, вторая правая вертикаль-
ная ось). У пузырьков, попавших в область, занятую уединенной вол-
ной, суммарные приток и отток теплоты уравниваются. Это возможно
потому, что колебания пузырька нелинейные. При этом фаза сжатия
пузырька, как известно, короче фазы расширения, в результате чего
общее количество теплоты, отданное пузырьком в фазе сжатия, может
быть равно общему количеству теплоты, полученного им в фазе рас-
ширения. В этом случае не происходит рассеивания внутренней энер-
гии газа и пузырек находится в тепловом равновесии с окружающей
жидкостью. Следовательно, амплитуда уединенной волны стабилизи-
руется за счет фоновой теплоты жидкого термостата.
Действительно, на рис. 4,
б
показан результат взаимодействия ди-
намических и тепловых процессов при осцилляциях газовых пузырь-
ков. Пунктирная кривая относится к градиенту температуры, жирная
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 1
17


