сплошная линия — к радиальной скорости стенки (левая вертикаль-
ная ось, точка означает производную по времени) в момент времени
t
= 212
,
4
мс. Тепловой поток
q
связан с градиентом температуры на
стенке соотношением
q
=
−
κ
(
T
)(
∂T/∂r
)
|
r
=
R
. Как следует из графи-
ков, у пульсирующего пузырька знак градиента температуры на стенке
тесно коррелирован со знаком скорости стенки, т.е. сдвиг фазы между
ними практически отсутствует. Оценки показывают, что характерное
время тепловой релаксации больше периода сжатия–расширения пу-
зырька. При расширении газ в окрестности стенки охлаждается, так
как теплопроводность не успевает компенсировать это охлаждение
пристенных слоев газа. В результате градиент температуры положи-
телен и теплота втекает из жидкости в газ. И наоборот, при сжатии
газ нагревается, скорость отрицательна, градиент температуры отри-
цателен и газ отдает теплоту в жидкость — это эффект движущейся
границы [24].
В эксперименте измерение сигналов датчиками проводят в выбран-
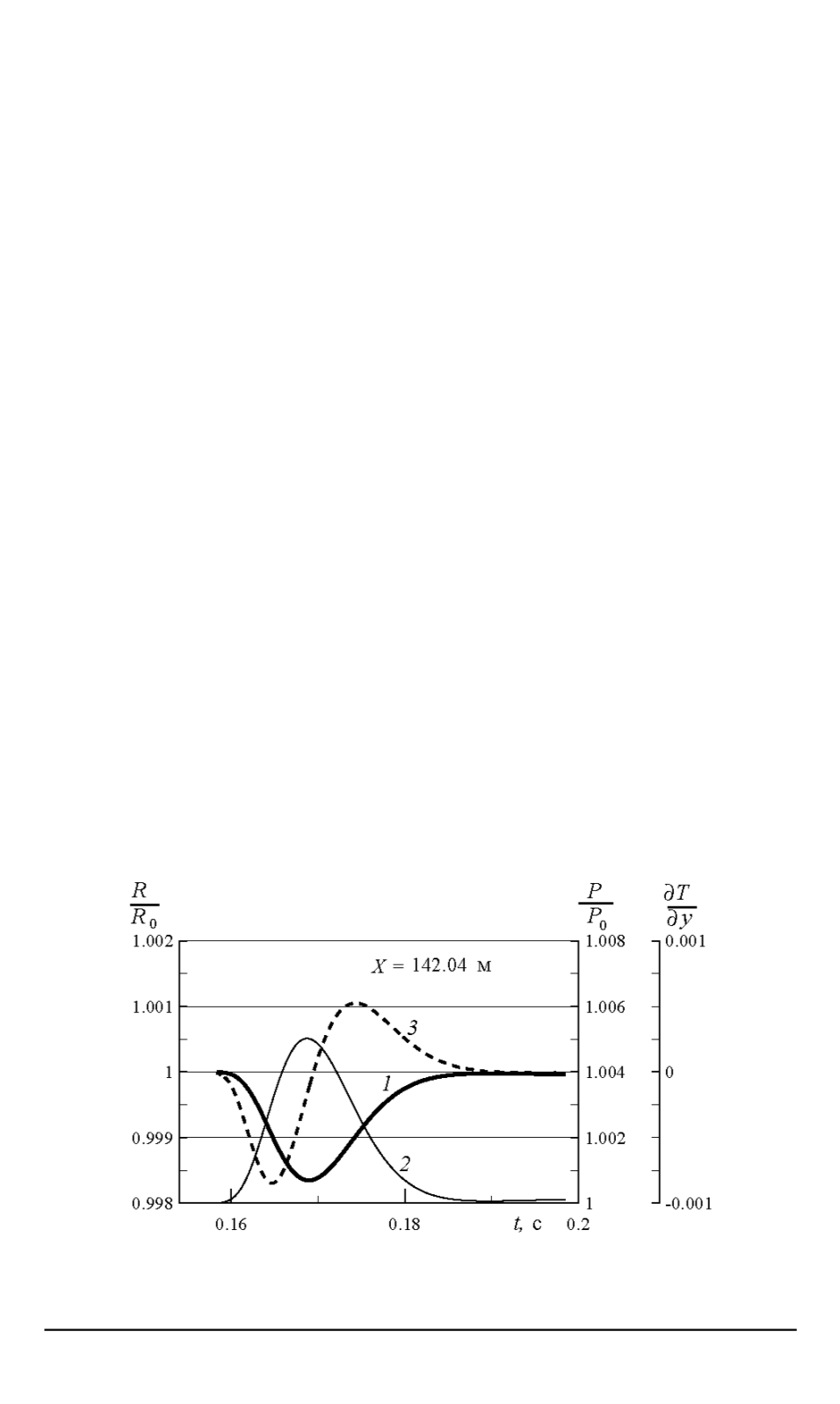
ной точке. Рассмотрим осциллограмму волнового процесса, снятую в
пространственной точке, например
X
= 142
,
04
м и показанную на
рис. 5. Пока проходит уединенная волна давления (кривая
2
), радиу-
сы пузырьков (кривая
1
) меньше начального значения. Как следует
из рис. 5, знак градиента температуры зависит от фазы колебания пу-
зырька, т.е. сжатия или расширения. На переднем фронте импульса
давления пузырек сжимается, производная температуры на поверхно-
сти стенки (кривая
3
) у него отрицательна и теплота отдается газом
в жидкость, а на спаде импульса давления, наоборот, — пузырек на-
чинает расширяться, производная температуры на стенке становится
Рис. 5. Временные профили в точке
X
= 142
,
04
м безразмерного радиуса
R
(
1
),
давления
P
(
2
) и безразмерного градиента температуры
(
∂T/∂y
)
|
y
=1
на границе
фаз (
3
)
18
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 1


