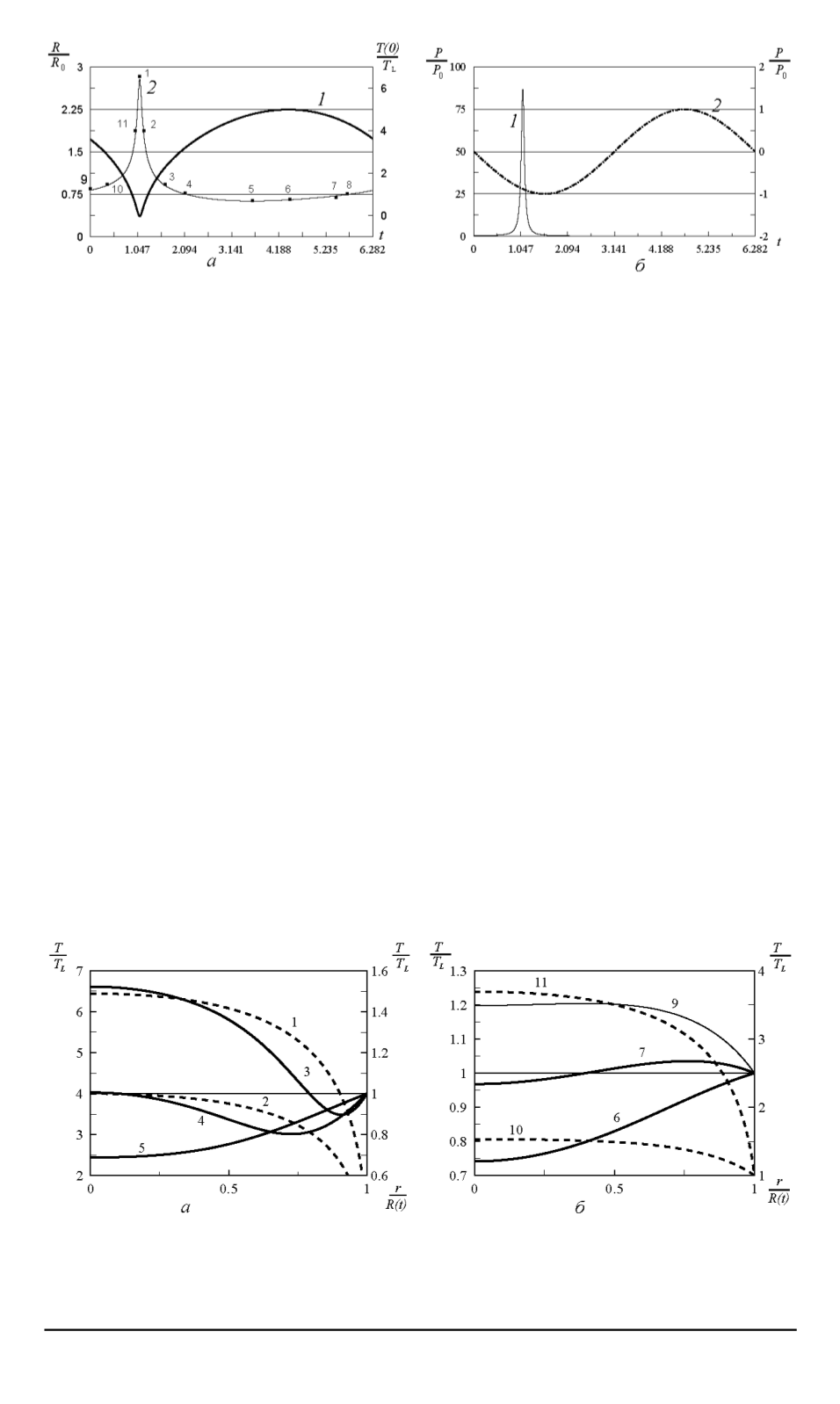
Рис. 1. Профили безразмерных радиуса, температуры и давления пузырька в
поле гармонической волны:
а
— радиус (
1
) и температура газа (
2
) в центре пузырька как функции безраз-
мерного времени;
b
— давление газа (
1
) и безразмерное давление гармонической
волны (
2
)
Получено хорошее, не только качественное, но и количественное, со-
гласие в пределах
20
%.
Тепловая динамика пульсирующего пузырька.
Первая рассмотрен-
ная в данной работе задача — изучение распределения температуры в
одиночном теплопроводящем пузырьке на стадиях сжатия и разреже-
ния под действием вынуждающего гармонического звукового поля.
Безразмерные временные профили температуры в центре (тонкая
линия) и радиуса (жирная линия) пузырька за один полный период ста-
ционарных вынужденных колебаний приведены на рис. 1,
а
(показан
один период колебаний). Здесь на кривой
2
точками и цифрами по-
казаны выбранные моменты безразмерного времени, а соответствую-
щие им температурные профили показаны на рис. 2. Сравнение кривой
нормированного радиуса с аналогичной кривой на рис. 3 из работы [6]
показывает хорошее качественное и количественное согласие. Кривая
температуры центра пузырька в работе [6] не приводится, но темпе-
ратурные профили для точек
А
,
В
и
С
, указанные на графике радиуса
Рис. 2. Радиальные профили температуры газа соответствующие фазе расши-
рения (
а
) и фазе сжатия (
б
) пузырька. Номера кривых соответствуют момен-
там безразмерного времени, указанным оцифрованными точками на кривой
2
рис. 1,
а
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2008. № 1
11


