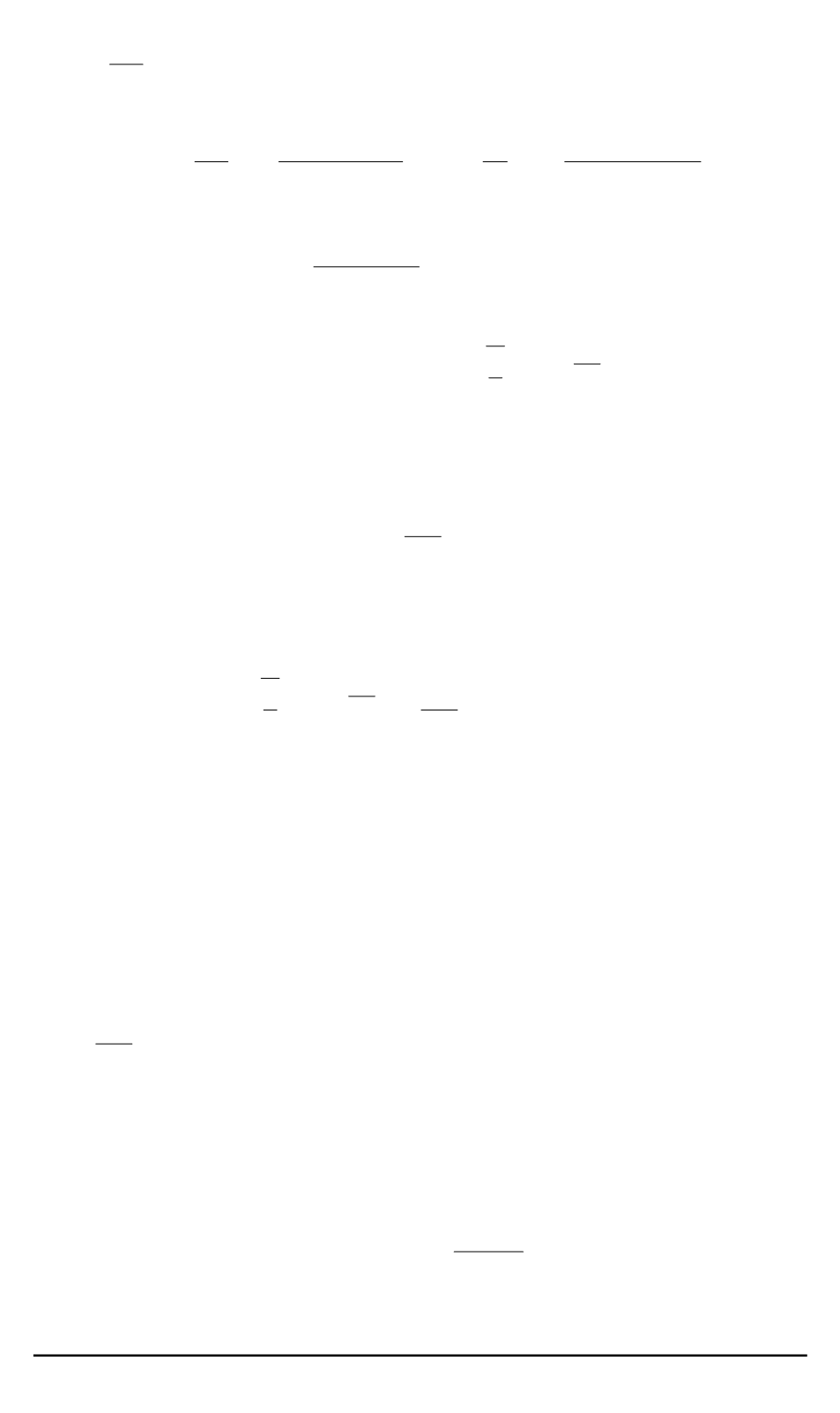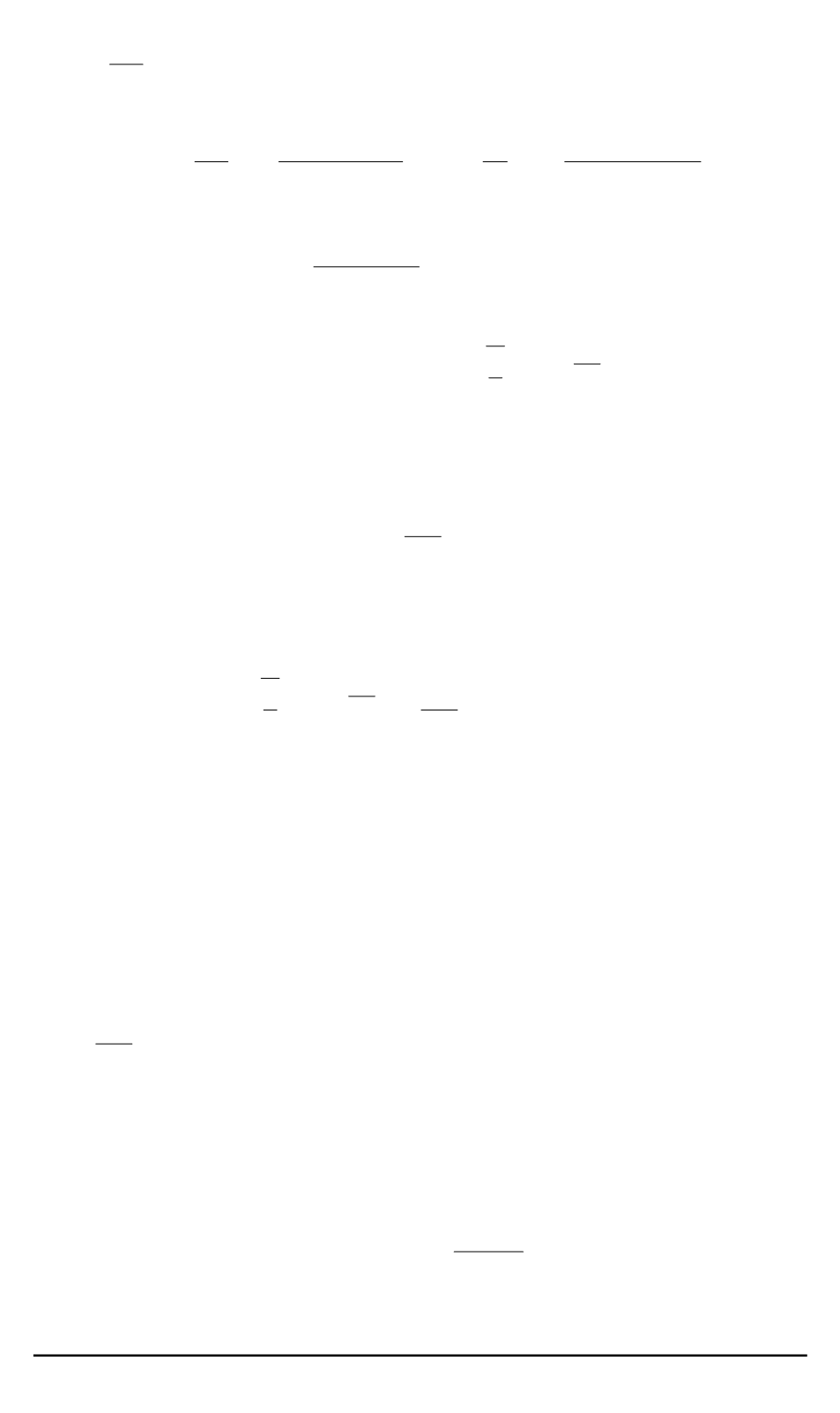
∞
X
α
2
=0
b
α
2
α
2
!
e
a/
(
α
2
+
μ
)
=
=
∞
X
α
2
=0
b
α
2
α
2
!
∞
X
k
=0
a
k
k
!(
α
2
+
μ
)
k
=
∞
X
k
=0
a
k
k
!
∞
X
α
2
=0
b
α
2
α
2
!(
α
2
+
μ
)
k
=
=
e
b
+
∞
X
k
=1
a
k
k
!(
k
−
1)!
∞
Z
0
v
k
−
1
e
−
μv
+
be
−
v
dv
=
=
e
b
+
∞
Z
0
r
a
v
I
1
(2
√
av
)
e
−
μv
+
be
−
v
dv.
(16)
Из известного представления функции Бесселя
I
1
(
z
) =
I
−
1
(
z
) =
1
2
πi
I
0+
e
(
z/
2)(
u
+1
/u
)
du
нетрудно получить
r
a
v
I
1
(2
√
av
) =
1
2
πi
I
0+
e
vu
+
a/u
du.
(17)
Подставляя уравнение (17) в формулу (16), и (16) в выражение (15),
получаем окончательно
F
(
t
;
z
1
, z
2
;
s
1
, s
2
) =
∞
Z
0
∞
Z
0
e
z
1
s
1
e
−
(
x
+
μ
)
t
+
z
2
e
z
2
(
s
2
−
1)
e
−
y
+
+
∞
Z
0
1
2
πi
I
0+
e
z
1
μ
(1
−
e
−
(
x
+
μ
)
t
)
/u
+
z
2
(
s
2
−
1)
e
−
y
−
v
+(
u
−
μ
)
v
du dv H
(
x, y
)
dxdy.
(18)
Из определения двойной производящей функции (6), формулы (18)
и разложения экспоненты
e
z
1
s
1
+
z
2
s
2
=
∞
X
α
1
,α
2
=0
z
α
1
1
z
α
2
2
α
1
!
α
2
!
s
α
1
1
s
α
2
2
следует интегральное представление (10). Теорема 1 доказана.
10
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2006. № 2