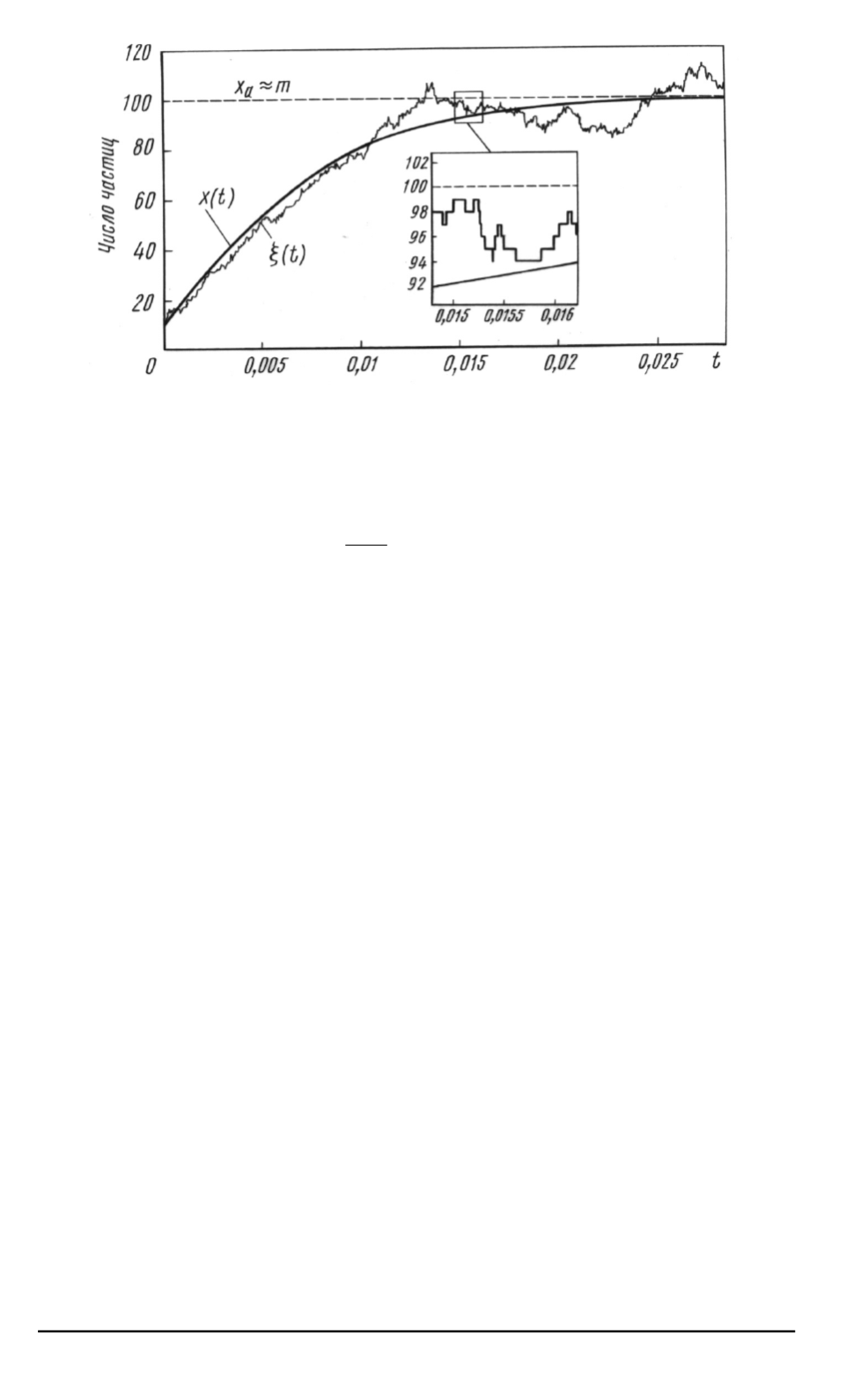
Рис
. 1.
Стохастическая реализация марковского процесса
ξ
(
t
)
и его детермини
-
рованное приближение
x
(
t
)
при начальных условиях
ξ
(0) = 10
, x
0
= 10
и значе
-
ниях параметров
λ
= 10
4
, µ
= 1
Решение уравнения
(1)
имеет вид логистической кривой с горизон
-
тальной асимптотой
x
a
=
p
λ/µ
(
рис
. 1).
Это означает
,
что при
t
→ ∞
система приходит в состояние равновесия
,
которое наступает при числе
частиц
,
близком к
x
a
.
Для системы частиц со схемой взаимодействий
0
→
T
,
2
T
→
T
рас
-
смотрим стохастическую модель в виде однородного во времени мар
-
ковского процесса
ξ
(
t
)
со счетным множеством состояний
N
=
{
0
,
1
, . . .
}
и непрерывным временем
t
∈
[0
,
∞
)
[8].
Событие
{
ξ
(
t
) =
i
}
означает
наличие в системе
i
частиц типа
T
в момент времени
t
.
Время нахо
-
ждения процесса в состоянии
i
случайно и длится либо до момента
появления новой частицы
,
либо до момента взаимодействия пары ча
-
стиц
.
Обозначим
P
ij
(
t
) = P
{
ξ
(
t
) =
j
|
ξ
(0) =
i
}
,
i, j
∈
N
,
вероятно
-
сти перехода процесса за время
t
из состояния
i
в состояние
j
.
Будем
считать
,
что вероятность
P
i,i
+1
(∆
t
)
образования одной частицы за до
-
статочно малое время
∆
t
равна
λ
∆
t
+
o
(∆
t
)
,
а вероятность
P
i,i
−
1
(∆
t
)
взаимодействия пары частиц пропорциональна числу
C
2
i
сочетаний
двух частиц из имеющихся
i
частиц и равна
µi
(
i
−
1)∆
t
+
o
(∆
t
)
,
где
λ
и
µ
—
заданные коэффициенты пропорциональности
.
Вероятность
рождения или гибели более одной частицы за время
∆
t
равна
o
(∆
t
)
.
Тогда полная вероятность
[9]
перехода из состояния
i
в состояние
j
за
время
t
+ ∆
t
с точностью до
o
(∆
t
)
определяется равенствами
P
00
(
t
+ ∆
t
) =
P
00
(
t
)(1
−
λ
∆
t
)
,
P
i
0
(
t
)
≡
0
, i
= 1
,
2
, . . . ,
P
ij
(
t
+ ∆
t
) =
P
i,j
−
1
(
t
)
λ
∆
t
+
P
ij
(
t
)(1
−
(
λ
+
µj
(
j
−
1))∆
t
) +
+
P
i,j
+1
(
t
)
µj
(
j
+ 1)∆
t,
i
= 0
,
1
, . . . , j
= 1
,
2
, . . . ,
(2)
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
1
5


