Используя разложение по формуле Тейлора
r
1 +
γ
ν
(
τ
)
a
2
= 1 +
ωτ
2
a
2
σ
ν
+
(1
−
2
a
2
)
τ
2
8
a
4
σ
2
ν
+
o
(
σ
−
2
ν
)
,
получим выражение
ϕ
ν
(
τ
)
∼
exp
µ
ωτ
ν/a
−
m
ν
σ
ν
−
1
2
µ
1
−
1
2
a
2
¶
ν
a
τ
2
σ
2
ν
¶
.
(28)
Покажем
,
что первое слагаемое под знаком экспоненты в выраже
-
нии
(28)
стремится к нулю
.
Действительно
,
из формул
(23)
и
(25)
сле
-
дует
m
ν
−
ν
a
=
ν
a
µ
I
0
(2
aν
)
−
I
1
(2
aν
)
I
1
(2
aν
)
¶
∼
1
4
a
2
,
откуда
m
ν
−
ν/a
=
o
(
σ
ν
)
.
Учитывая асимптотику для
σ
2
ν
в утвержде
-
нии
2,
получаем окончательно
ϕ
ν
(
τ
)
∼
exp
µ
−
1
2
µ
1
−
1
2
a
2
¶
ν
a
τ
2
σ
2
ν
¶
∼
e
−
τ
2
/
2
.
Теорема доказана
.
Решение стационарного уравнения в случае
p
0
2
>
0
,
p
0
2
p
2
0
<
1
.
Предельная теорема
.
Схема взаимодействий в данном случае прини
-
мает вид
0
→
k
0
T
,
k
0
= 1
,
2
;
2
T
→
k
2
T
,
k
2
= 0
,
1
.
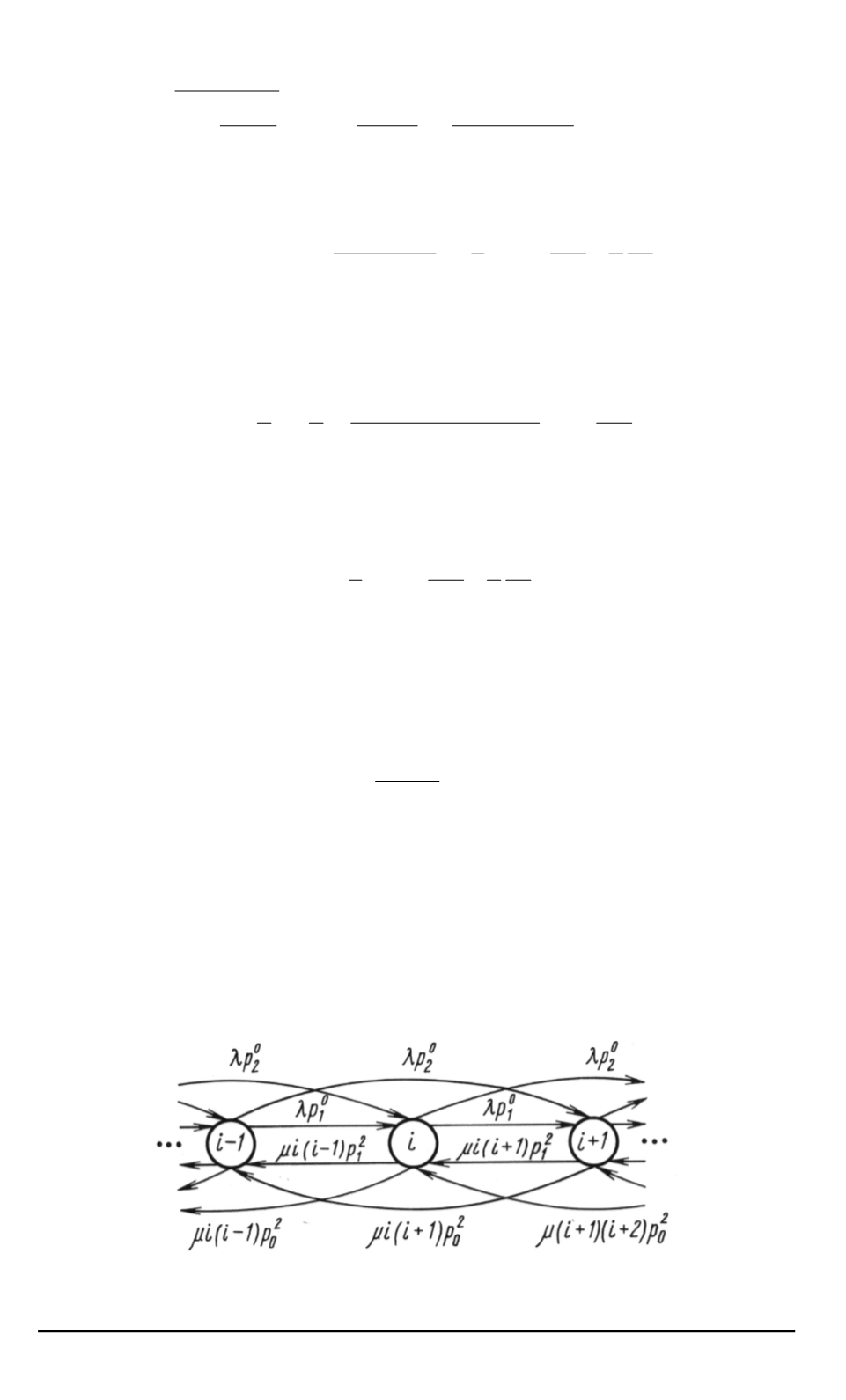
Возможные переходы
между состояниями марковского процесса
ξ
(
t
)
показаны на рис
. 4.
Введем обозначения
ν
=
p
λp
0
2
/µ
,
a
= (1
−
p
0
2
p
2
0
)
/
2
p
0
2
.
С помощью
замены переменных
z
= 2
ν
(
s
+
p
2
0
)
,
y
(
z
) = (
s
+
p
2
0
)
−
1
e
νs
f
(
s
)
стацио
-
нарное уравнение
(9)
сводится к вырожденному гипергеометрическому
уравнению
zy
00
+ (2
−
z
)
y
0
−
(1 +
aν
)
y
= 0
[12,
гл
. 6, § 1,
уравнение
(2)].
Аналитическое на всей комплексной плоскости решение этого уравне
-
ния имеет вид
y
(
z
) =
C
Φ(1 +
aν,
2;
z
)
,
Рис
. 4.
Диаграмма переходов в случае
p
0
2
>
0
, p
0
2
p
2
0
<
1
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
1
15


