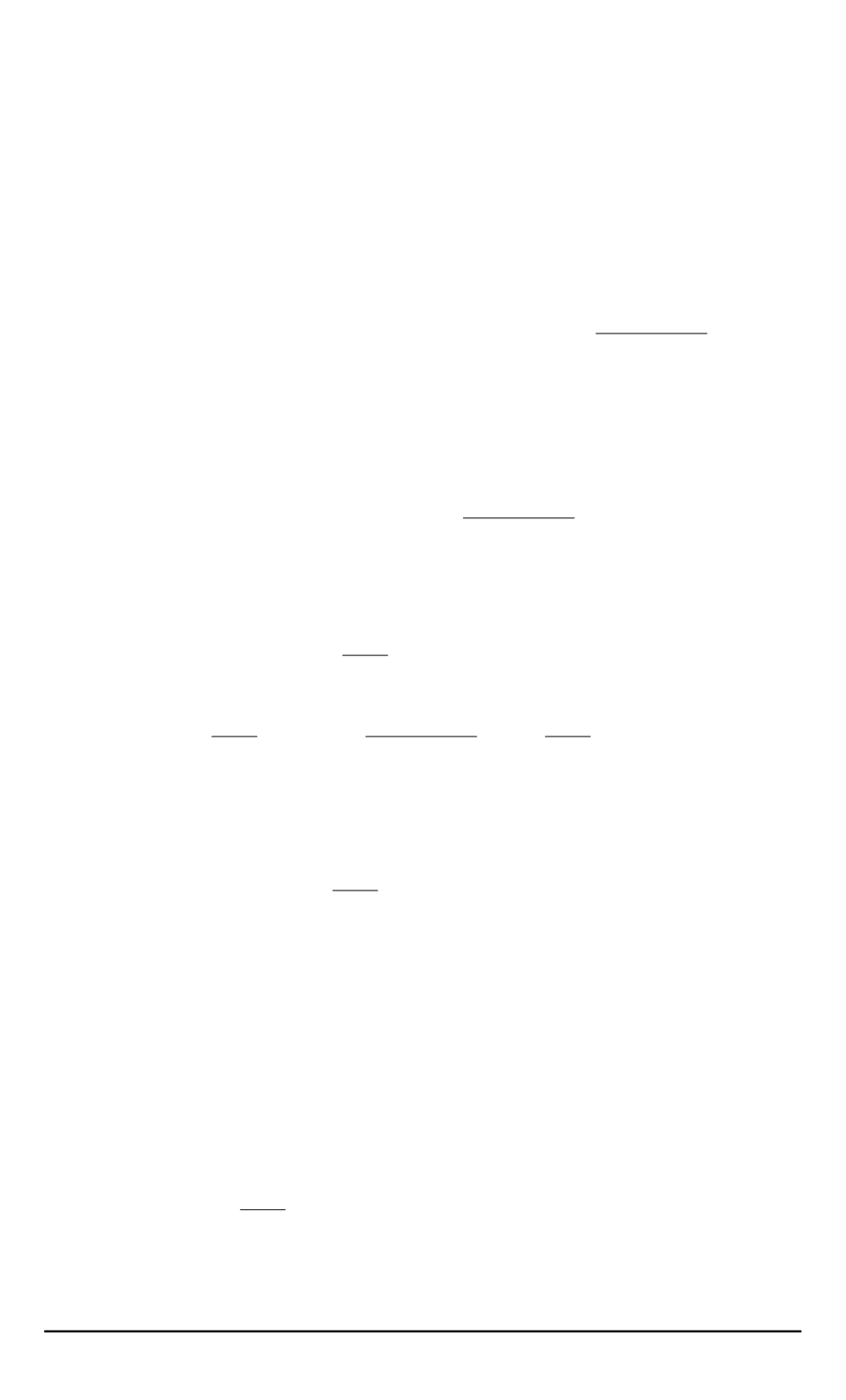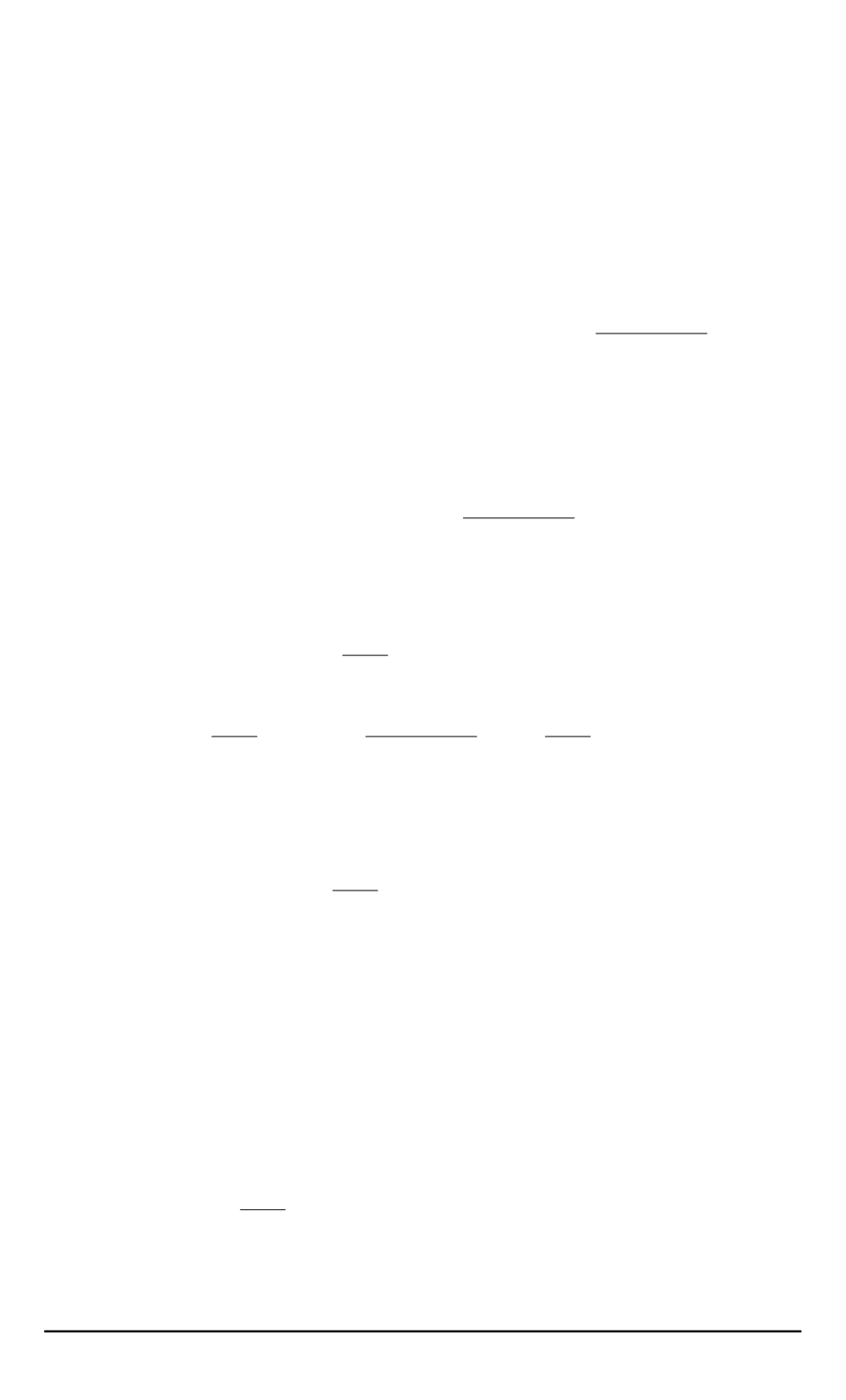
Следовательно
,
δs
∗
ij
e
∗
ij
= ¯
ε
и
δ
¯
σ
и
=
δ
µ
¯
σ
и
Z
0
¯
ε
и
(
ξ
)
dξ
¶
.
Второе слагаемое в правой части выражения
(14)
принимает вид
δs
∗
ij
¯
εα
ij
=
δ
(
σ
ij
−
¯
σβ
ij
)¯
εα
ij
=
= ¯
εδ
(
σ
ij
α
ij
−
¯
σβ
ij
α
ij
) = ¯
εδ
µ
¯
σ
−
¯
σ
C
ijkl
α
kl
α
ij
C
ijkl
α
kl
α
ij
¶
= 0
.
Третье слагаемое в правой части выражения
(14)
принимает вид
δ
¯
σβ
ij
e
∗
ij
=
δ
¯
σβ
ij
(
ε
ij
−
¯
εα
ij
) =
=
δ
¯
σ
µ
β
ij
ε
ij
−
¯
ε
C
ijkl
α
kl
α
ij
C
ijkl
α
kl
α
ij
¶
=
δ
¯
σ
(¯
ε
−
¯
ε
) = 0
.
Последнее слагаемое в правой части выражения
(14)
принимает вид
δ
¯
σβ
ij
¯
εα
ij
=
δ
¯
σ
µ
¯
σ
3
K
∗
+ ¯
ε
т
¶
β
ij
α
ij
=
=
Ã
¯
σδ
¯
σ
3
K
∗
+ ¯
ε
т
δ
¯
σ
!
C
ijkl
α
kl
α
ij
C
ijkl
α
kl
α
ij
=
δ
µ
¯
σ
2
6
K
∗
+ ¯
ε
т
¯
σ
¶
.
Окончательно имеем
δR
=
δ
Z
Ω
µ
¯
σ
2
6
K
∗
+ ¯
ε
т
¯
σ
+
¯
σ
и
Z
0
¯
ε
и
(
ξ
)
dξ
¶
dV .
Введем величину
O
такую
,
что
δO
=
δR
−
δ
Z
S
2
σ
ij
n
j
¯
u
i
dS
= 0
.
Величина
O
имеет вид
O
(
σ
ij
) =
Z
Ω
µ
¯
σ
2
6
K
∗
+ ¯
ε
т
¯
σ
+
¯
σ
и
Z
0
¯
ε
и
(
ξ
)
dξ
¶
dV
−
Z
S
2
σ
ij
n
j
¯
u
i
dS.
(15)
50
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
1