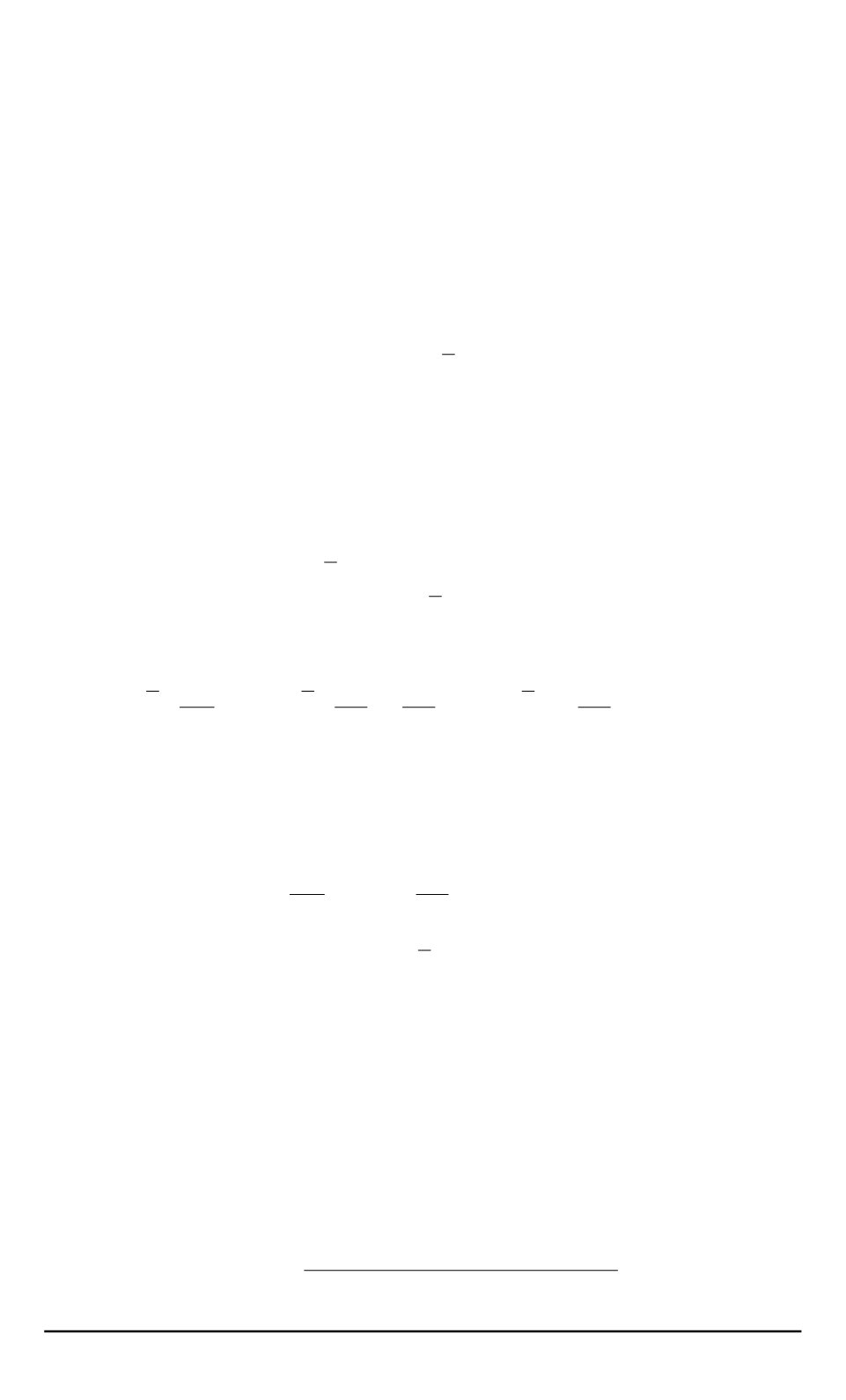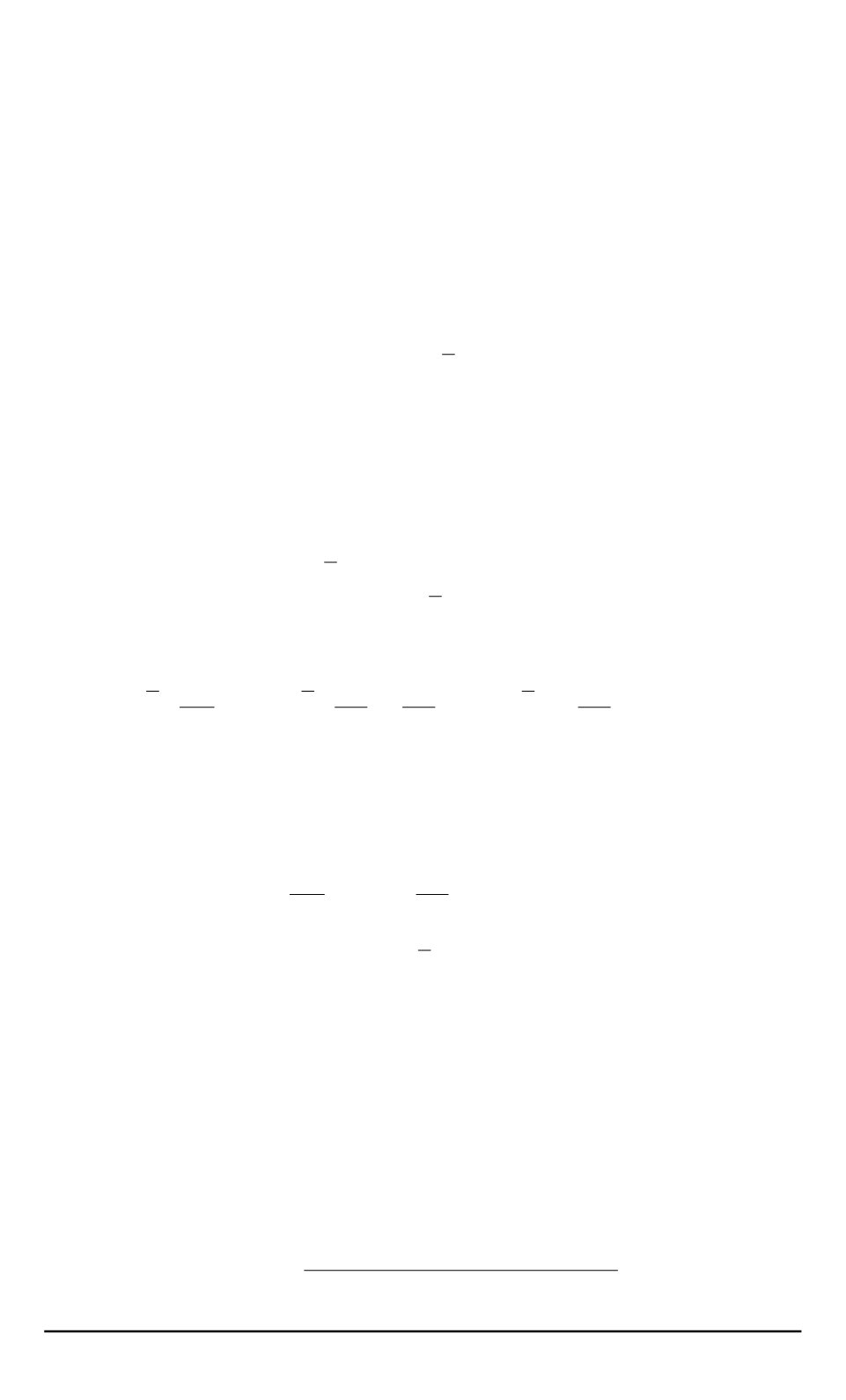
Для материалов
,
одинаково сопротивляющихся растяжению и сжа
-
тию
,
постулируется существование инвариантной к виду напряженно
-
го состояния зависимости между обобщенными интенсивностями на
-
пряжений и деформаций
:
¯
σ
и
= ¯
σ
и
(¯
ε
и
, T
)
,
(
4
)
которая определяется экспериментально
.
При заданной температуре
переход материала из упругого состояния в пластическое происходит
при одном и том же значении
¯
σ
и
= ¯
σ
и
0
.
Для упругой изотропной среды тензор
α
имеет только диагональные
компоненты
α
11
=
α
22
=
α
33
= 1
/
√
3
.
Отличные от нуля компоненты
тензора
C
упругих постоянных имеют вид
C
1122
=
C
2211
=
C
1133
=
C
3311
=
C
2233
=
C
3322
=
K
−
2
G/
3
,
C
1111
=
C
2222
=
C
3333
=
K
+ 4
G/
3
,
где
K
и
G
—
модули всестороннего сжатия и сдвига материала
.
При
этом
K
∗
=
K
,
¯
σ
=
σ
kk
/
√
3
,
тензор
β
имеет только диагональные ком
-
поненты
β
11
=
β
22
=
β
33
= 1
/
√
3
.
Соответственно
,
выражение
(1)
приобретает вид
√
3
µ
σ
kk
3
¶
= 3
√
3
µ
ε
kk
3
−
ε
т
kk
3
¶
= 3
√
3
K
µ
ε
kk
3
−
d
∆
T
¶
,
соответствующий приведенному в работе
[11]
линейному выражению
для связи между средним нормальным напряжением и относительным
изменением объема
:
σ
kk
3
= 3
K
µ
ε
kk
3
−
d
∆
T
¶
,
обе части которого умножены на
√
3
;
d
—
коэффициент линейного рас
-
ширения материала
.
Константы
α
ij
определяются из трех экспериментов на одноосное
напряженное состояние и трех на простой сдвиг
.
Пусть при заданной
температуре известны три значения
σ
iiY
предела текучести при растя
-
жении вдоль каждой оси анизотропии и три значения
σ
iiS
предела те
-
кучести при сдвиге по площадкам
,
направление которого совпадает с
направлениями анизотропии материала
.
Тогда константы
α
ij
определя
-
ются из следующей системы уравнений
:
¯
σ
и
0
=
q
(3
K
∗
B
1111
−
α
11
α
11
)
σ
11
Y
σ
11
Y
,
44
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
1