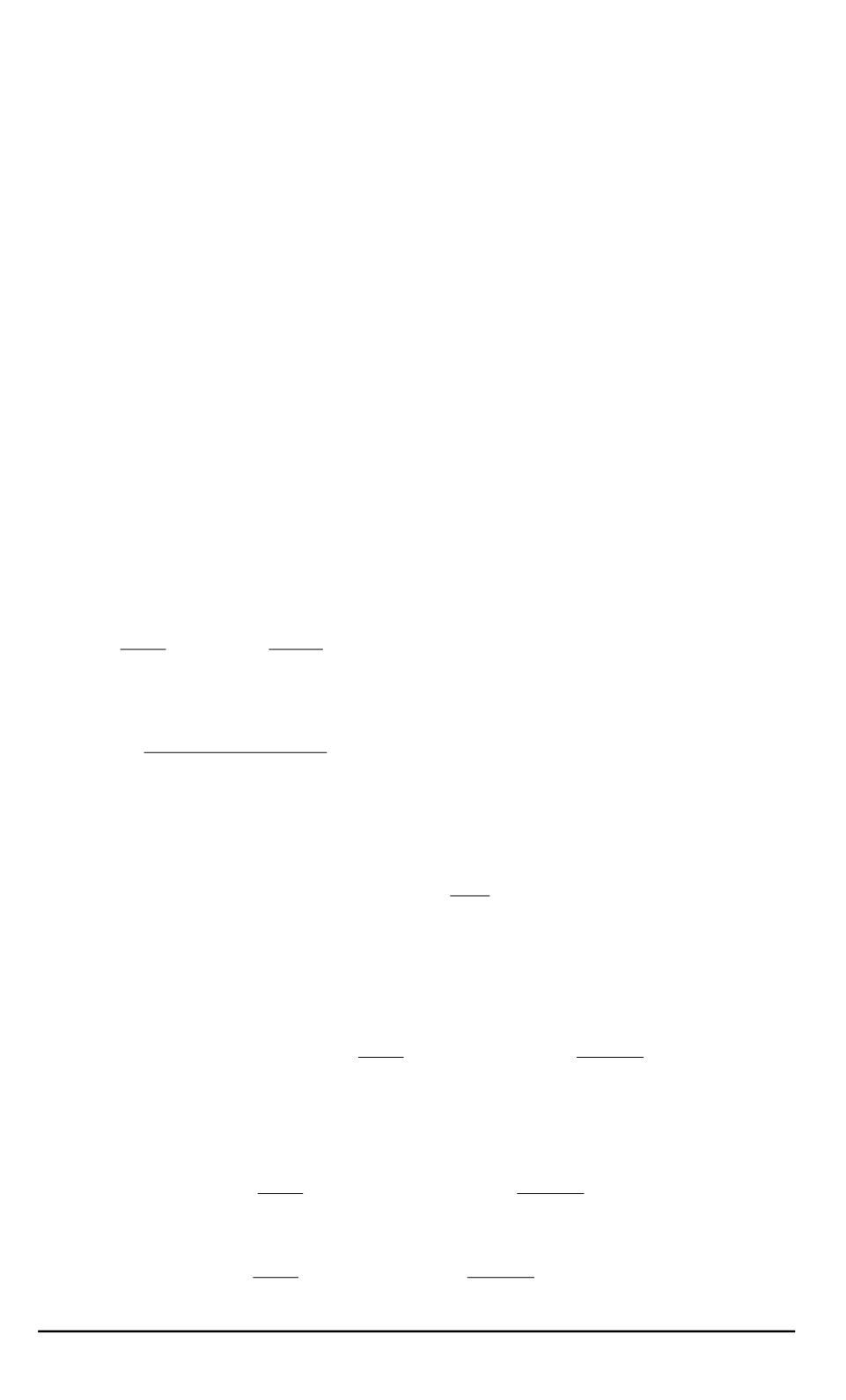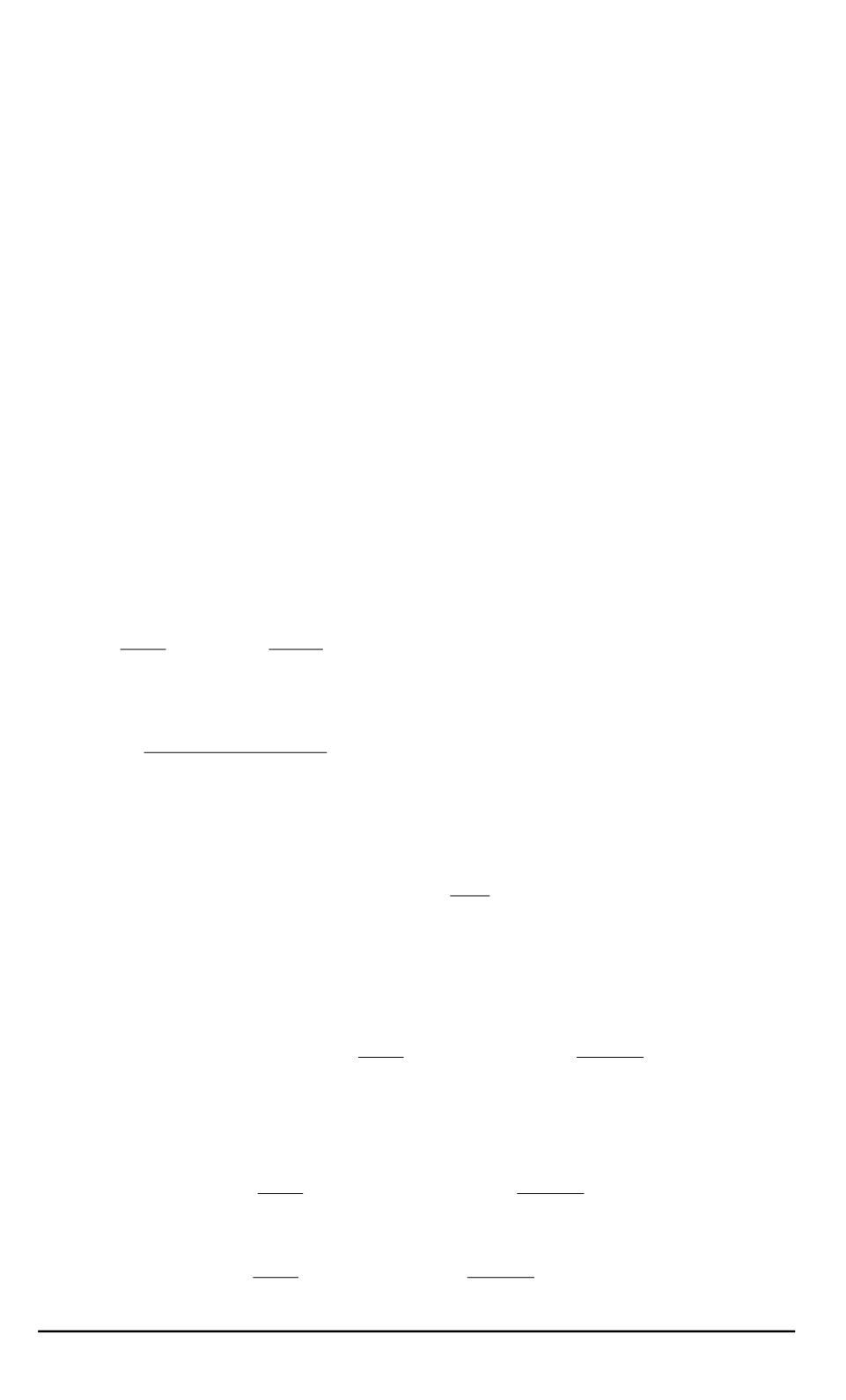
Функционал
(15)
может рассматриваться только на полях напряже
-
ний
,
удовлетворяющих уравнениям равновесия и граничным условиям
,
налагаемым на напряжения на участках
S
1
.
Легко доказать
,
что при указанных ограничениях для поля возмож
-
ных изменений величины
δσ
ij
уравнение
(13)
заменяет соотношения
Сен
-
Венана совместности деформаций
(
последние выполняются
,
если
справедливы соотношения
(6)
для деформаций и перемещений
)
и гра
-
ничные условия
,
налагаемые на перемещения на участках границы
S
2
,
которые
,
тем самым
,
становятся естественными
.
Следовательно
,
в
стационарной точке полученного функционала
(15)
также выполняют
-
ся соотношения Сен
-
Венана совместности деформаций и граничные
условия
,
налагаемые на перемещения
.
Выясним характер стационарной точки функционала
(15).
Для это
-
го найдем разность значений функционала
(15),
соответствующих ста
-
тически возможным
σ
ij
(
M
) =
σ
r
ij
(
M
) +
δσ
ij
(
M
)
и действительным
σ
r
ij
(
M
)
напряжениям
.
С учетом уравнения
(13)
имеем
∆
O
=
O
(
σ
ij
)
−
O
(
σ
r
ij
) =
=
Z
Ω
µ
¯
σ
2
6
K
∗
+ ¯
ε
т
¯
σ
−
(¯
σ
r
)
2
6
K
∗
−
¯
ε
т
¯
σ
r
+
¯
σ
и
Z
¯
σ
r
и
¯
ε
и
(
ξ
)
dξ
¶
dV
−
Z
S
2
δσ
ij
n
j
¯
u
i
dS
=
=
Z
Ω
µ
(¯
σ
−
¯
σ
r
) (¯
σ
+ ¯
σ
r
)
6
K
∗
+ ¯
ε
т
(¯
σ
−
¯
σ
r
)
−
ε
r
ij
δσ
ij
+
¯
σ
и
Z
¯
σ
r
и
¯
ε
и
(
ξ
)
dξ
¶
dV .
При малом отличии
¯
σ
и
от
¯
σ
r
и
приближенно получим
¯
ε
и
(¯
σ
и
) = ¯
ε
r
и
+
∂
¯
ε
r
и
∂
¯
σ
r
и
δ
¯
σ
и
.
Кроме того
,
согласно соотношениям
(1)–(3),
компоненты тензора
деформации имеют вид
ε
r
ij
= ¯
ε
r
α
ij
+
e
∗
r
ij
=
Ã
¯
σ
r
3
K
∗
+ ¯
ε
т
!
α
ij
+
s
∗
r
kl
3
K
∗
¯
ε
r
и
¯
σ
r
и
B
ijkl
.
Тогда
ε
r
ij
δσ
ij
=
Ã
¯
σ
r
3
K
∗
+ ¯
ε
т
!
α
ij
δσ
ij
+
s
∗
r
kl
3
K
∗
¯
ε
r
и
¯
σ
r
и
B
ijkl
δσ
ij
=
=
Ã
¯
σ
r
3
K
∗
+ ¯
ε
т
!
δ
¯
σ
+
s
∗
r
kl
3
K
∗
¯
ε
r
и
¯
σ
r
и
B
ijkl
δs
∗
kl
.
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
1
51