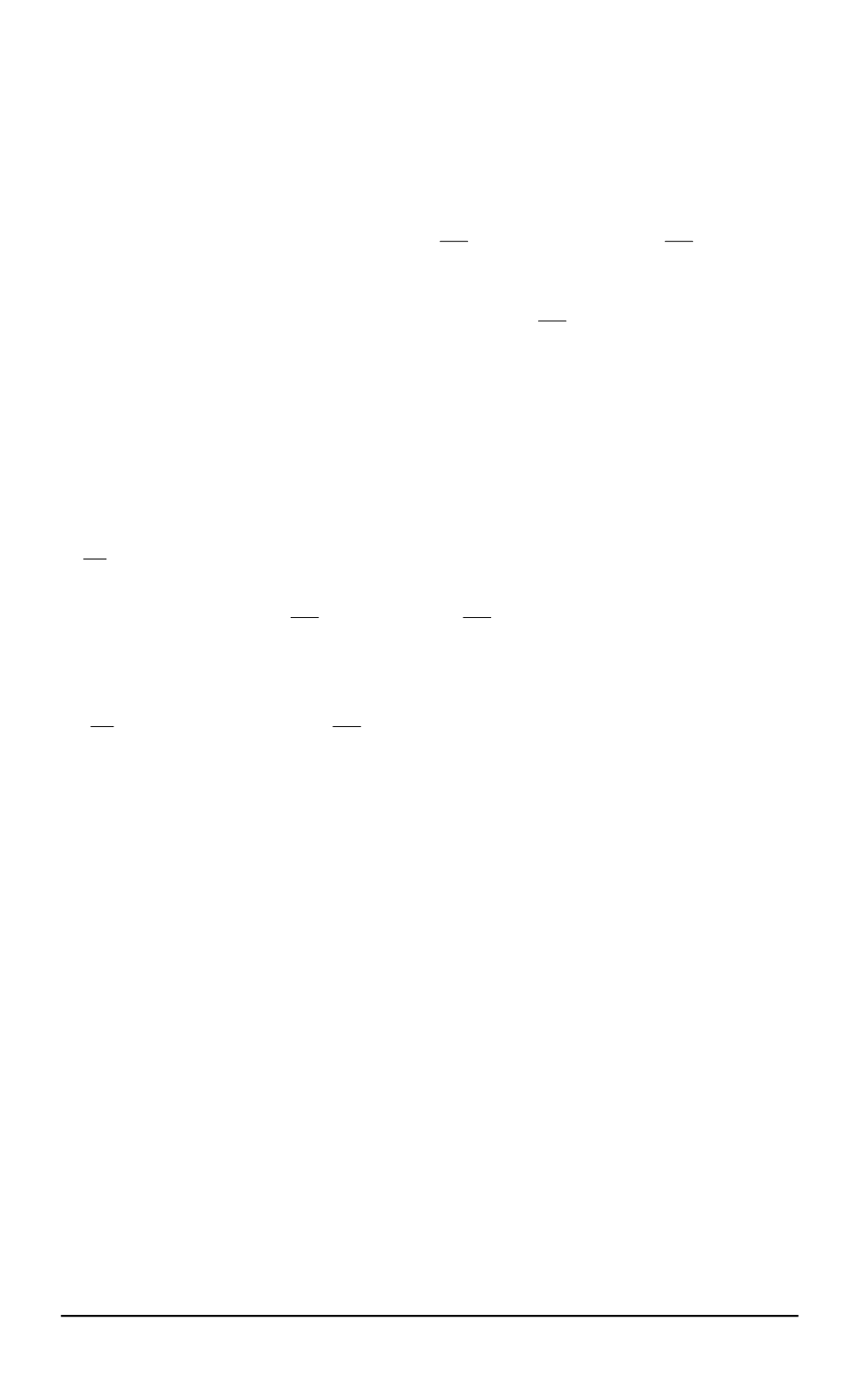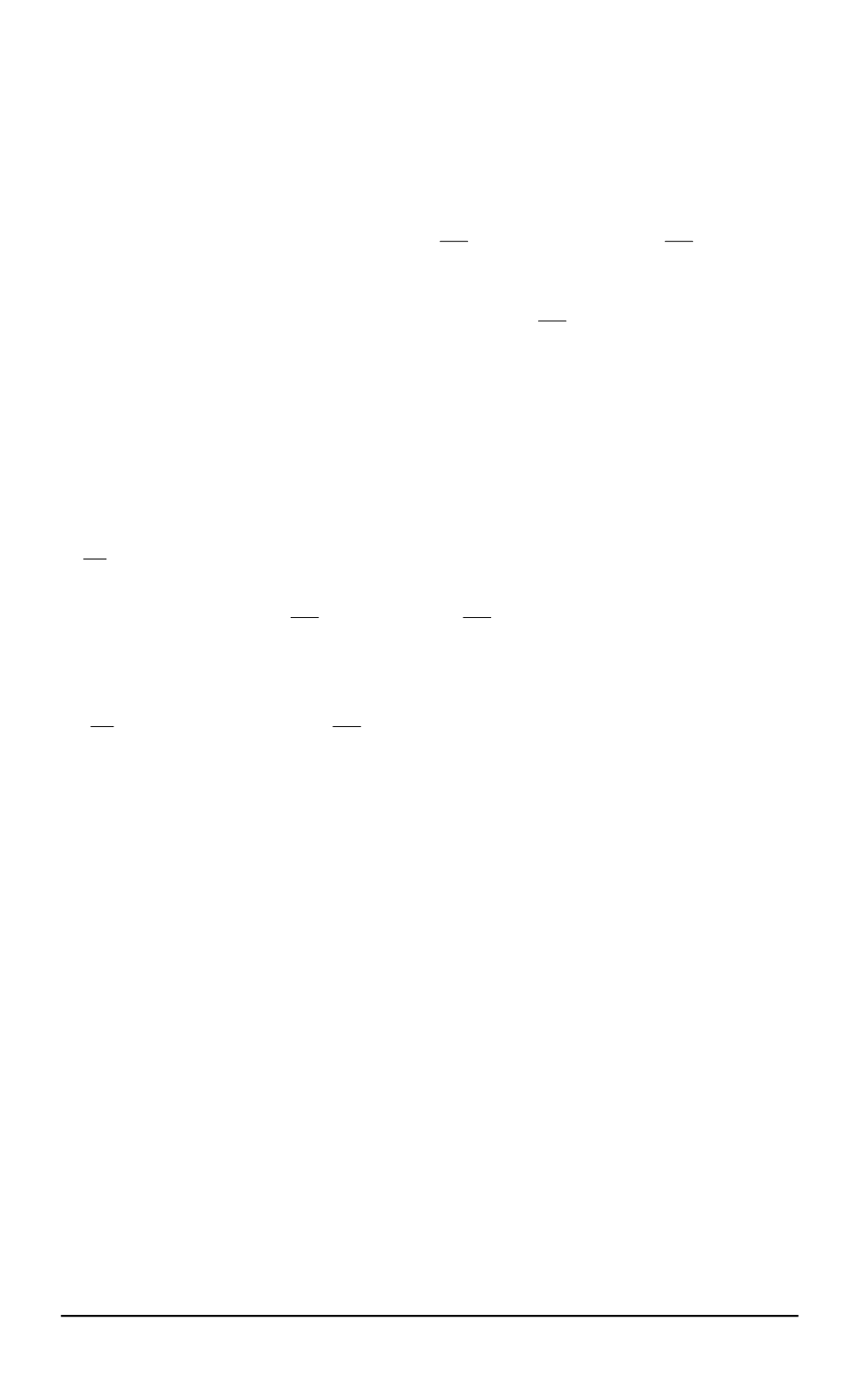
Полученные в правой части уравнения
(13)
суммы преобразуем
,
ис
-
пользуя определение производящей функции
(10):
∞
X
k
=0
x
k
kp
k
(
t
0
, t
) =
x
∞
X
k
=1
kx
k
−
1
p
k
(
t
0
, t
) =
=
x
∂
∂x
∞
X
k
=0
x
k
p
k
(
t
0
, t
) =
x
∂
∂x
ϕ
(
t
0
, t, x
)
,
∞
X
k
=0
x
k
(
k
+ 1)
p
k
+1
(
t
0
, t
) =
∞
X
k
=1
kx
k
−
1
p
k
(
t
0
, t
) =
∂
∂x
ϕ
(
t
0
, t, x
)
,
∞
X
k
=1
x
k
p
k
−
1
(
t
0
, t
) =
x
∞
X
k
=1
x
k
−
1
p
k
−
1
(
t
0
, t
) =
x
∞
X
k
=0
x
k
p
k
(
t
0
, t
) =
xϕ
(
t
0
, t, x
)
.
После подстановки полученных выражений в уравнение
(13)
пре
-
образуем его к виду
∂
∂t
ϕ
(
t
0
, t, x
) =
−
μ
(
t
)
ϕ
(
t
0
, t, x
)
−
−
λx
∂
∂x
ϕ
(
t
0
, t, x
) +
λ
∂
∂x
ϕ
(
t
0
, t, x
) +
μ
(
t
)
xϕ
(
t
0
, t, x
)
,
или после приведения подобных членов
—
к виду
∂
∂t
ϕ
(
t
0
, t, x
)
−
λ
(1
−
x
)
∂
∂x
ϕ
(
t
0
, t, x
) =
−
μ
(
t
)(1
−
x
)
ϕ
(
t
0
, t, x
)
.
(14)
Итак
,
решение системы обыкновенных дифференциальных уравне
-
ний
(6),
вообще говоря
,
бесконечномерной
,
свелось к интегрированию
линейного уравнения в частных производных с начальным
(12)
и гра
-
ничным
(11)
условиями
.
Отметим здесь
,
что численное интегрирование
уравнения
(14)
мало эффективно для достижения конечной цели
—
вы
-
числения распределения
p
k
(
t
0
, t
)
,
k
= 0
,
1
,
2
, . . .
.
Для этого необходимо
получить аналитическое
(
или
,
по крайней мере
,
в замкнутой форме
)
ре
-
шение уравнения
(14).
Следуя общей теории линейных
(
квазилинейных
)
дифференциаль
-
ных уравнений в частных производных
[4],
будем интерпретировать ре
-
шение уравнения в частных производных вида
(14)
с краевыми усло
-
виями
(11)
и
(12)
как отыскание интегральной поверхности
,
удовлетво
-
ряющей уравнению
(14)
и проходящей через заданную линию
.
Чтобы
воспользоваться традиционной схемой решения рассматриваемого ви
-
да дифференциального уравнения в частных производных
,
представим
начальное и граничное условия уравнения
(14)
в виде некоторой ли
-
нии в пространстве координат
(
t, x, ϕ
)
,
описываемой в параметриче
-
ской форме
.
98
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
3