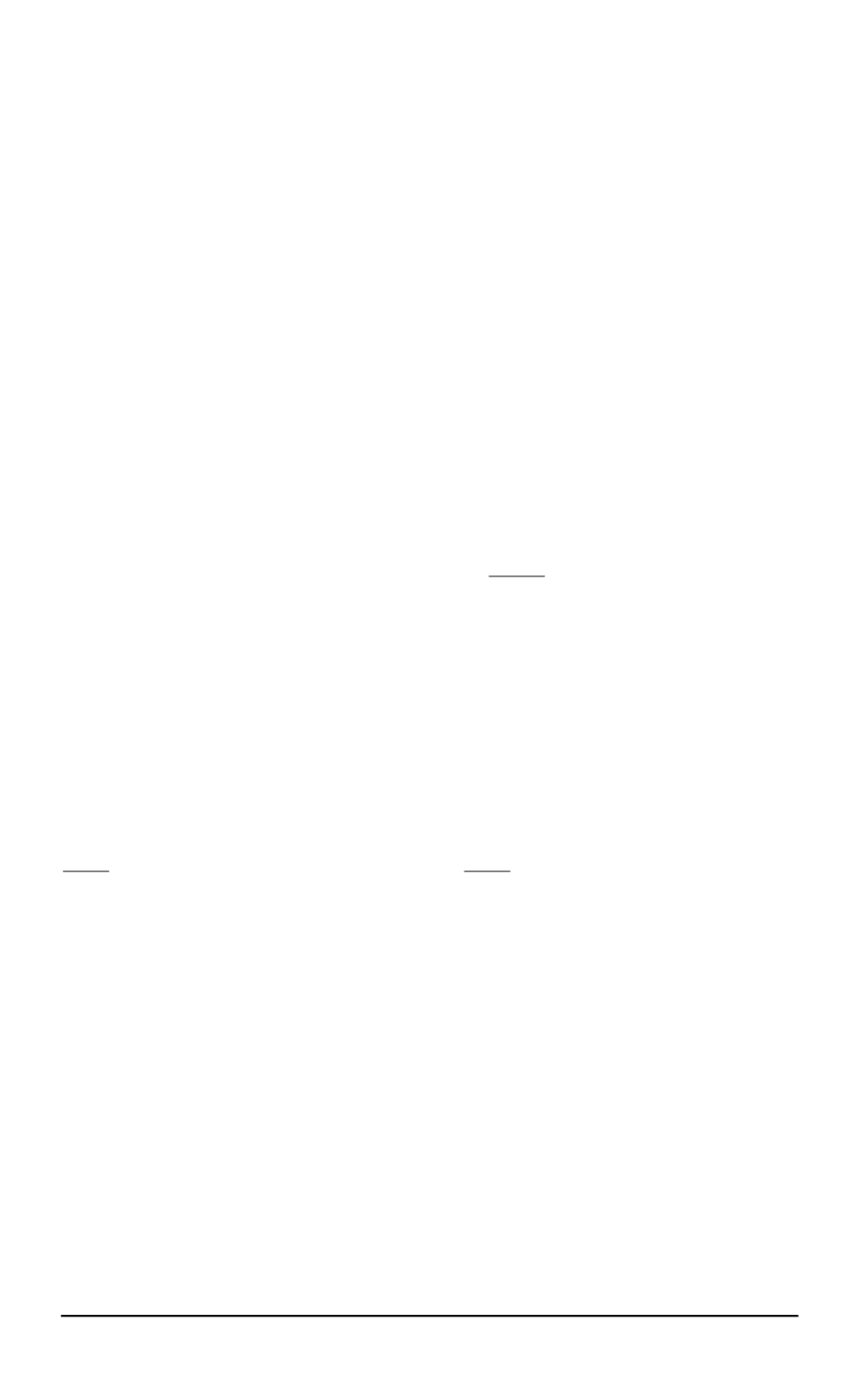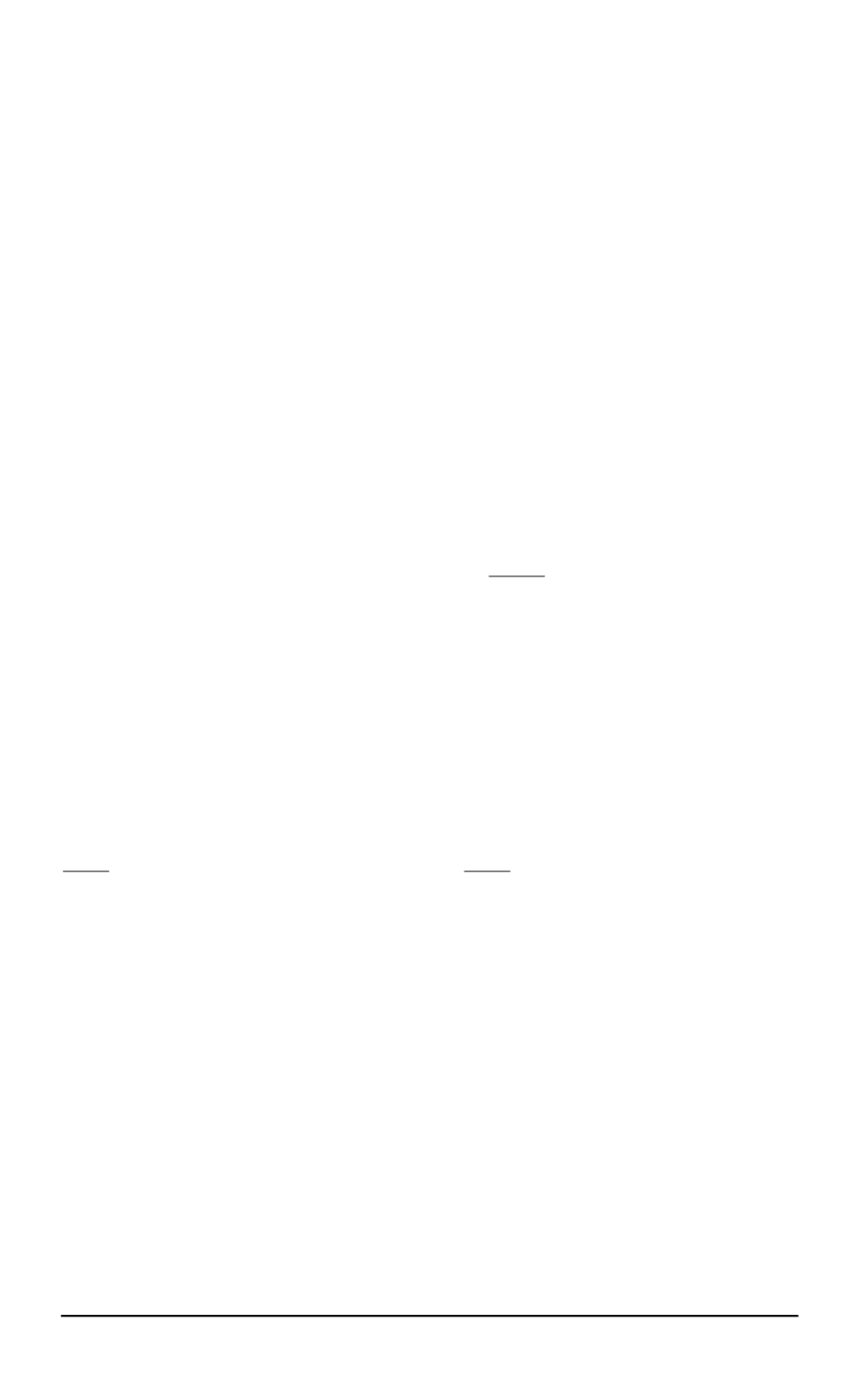
где
s
—
скалярный параметр
,
принимающий неотрицательные зна
-
чения
.
Система обыкновенных дифференциальных уравнений
(19)
инте
-
грируется с начальными условиями
(18),
т
.
е
.
t
(
s
)
|
s
=0
=
τ
0
(
z
)
,
x
(
s
)
|
s
=0
=
x
0
(
z
)
,
ϕ
0
(
s
)
|
s
=0
=
ϕ
0
(
z
)
.
(20)
Поскольку правые части системы обыкновенных дифференциаль
-
ных уравнений
(19)
не зависят в явном виде от
s
,
т
.
е
.
система авто
-
номна
,
то выбор начального значения
s
не существен
.
Для простоты
начальное значение
s
принимается равным нулю
.
Первые два уравнения системы
(19)
можно интегрировать незави
-
симо от третьего уравнения
:
t
(
s
;
z
) =
τ
0
(
z
) +
s,
ln
1
−
x
B
=
λs,
(21)
где
B
—
константа
,
зависящая от начального условия
,
а именно
B
=
= 1
−
x
0
(
z
)
,
следовательно
,
1
−
x
(
s, z
) = (1
−
x
0
(
z
))
e
λs
,
или
x
(
s, z
) = 1
−
(1
−
x
0
(
z
))
e
λs
.
(22)
Наконец
,
решая третье уравнение в системе
(16),
получим
dϕ
ϕ
(
s
)
=
−
μ
(
t
(
s
)) (1
−
x
(
s
))
ds,
или
ln
ϕ
(
s
)
C
=
−
s
Z
0
μ
(
t
(
s
0
) (1
−
x
(
s
0
))
ds
0
,
откуда
ϕ
(
s
) =
C
exp
−
s
Z
0
μ
(
t
(
s
0
) (1
−
x
(
s
0
))
ds
0
,
где
С
—
константа
,
зависящая от начального условия
C
=
ϕ
(
s
)
s
=0
,
или
C
=
ϕ
0
(
z
)
,
с уче
-
том чего имеем
ϕ
(
s, z
) =
ϕ
0
(
z
) exp
−
s
Z
0
μ
(
t
(
s
0
)) (1
−
x
(
s
0
, z
))
ds
0
.
(23)
Формулы
(21)–(23)
описывают в параметрической форме искомую
интегральную поверхность
,
проходящую через линию
(18).
100
ISSN 1812-3368.
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. “
Естественные науки
”. 2005.
№
3