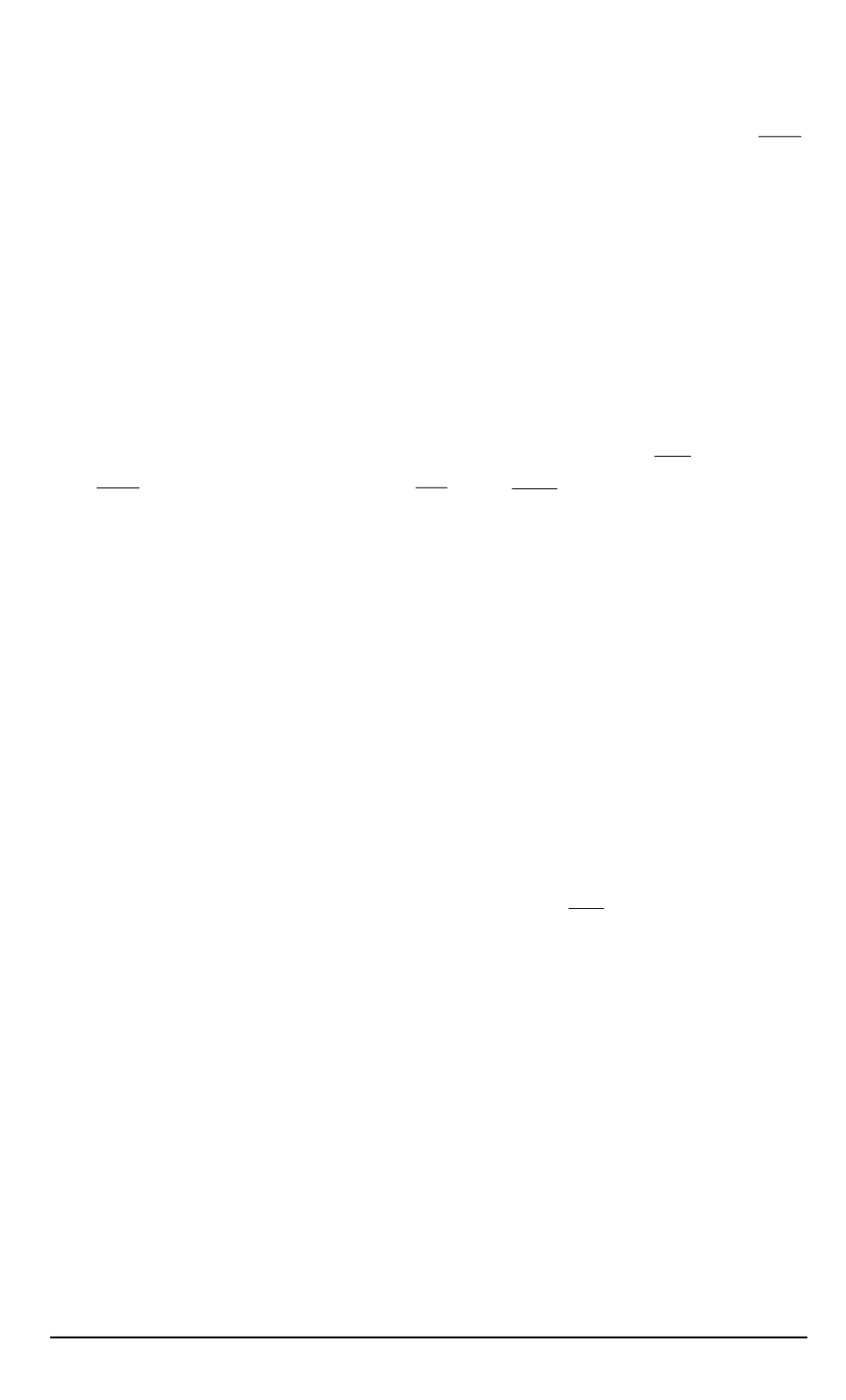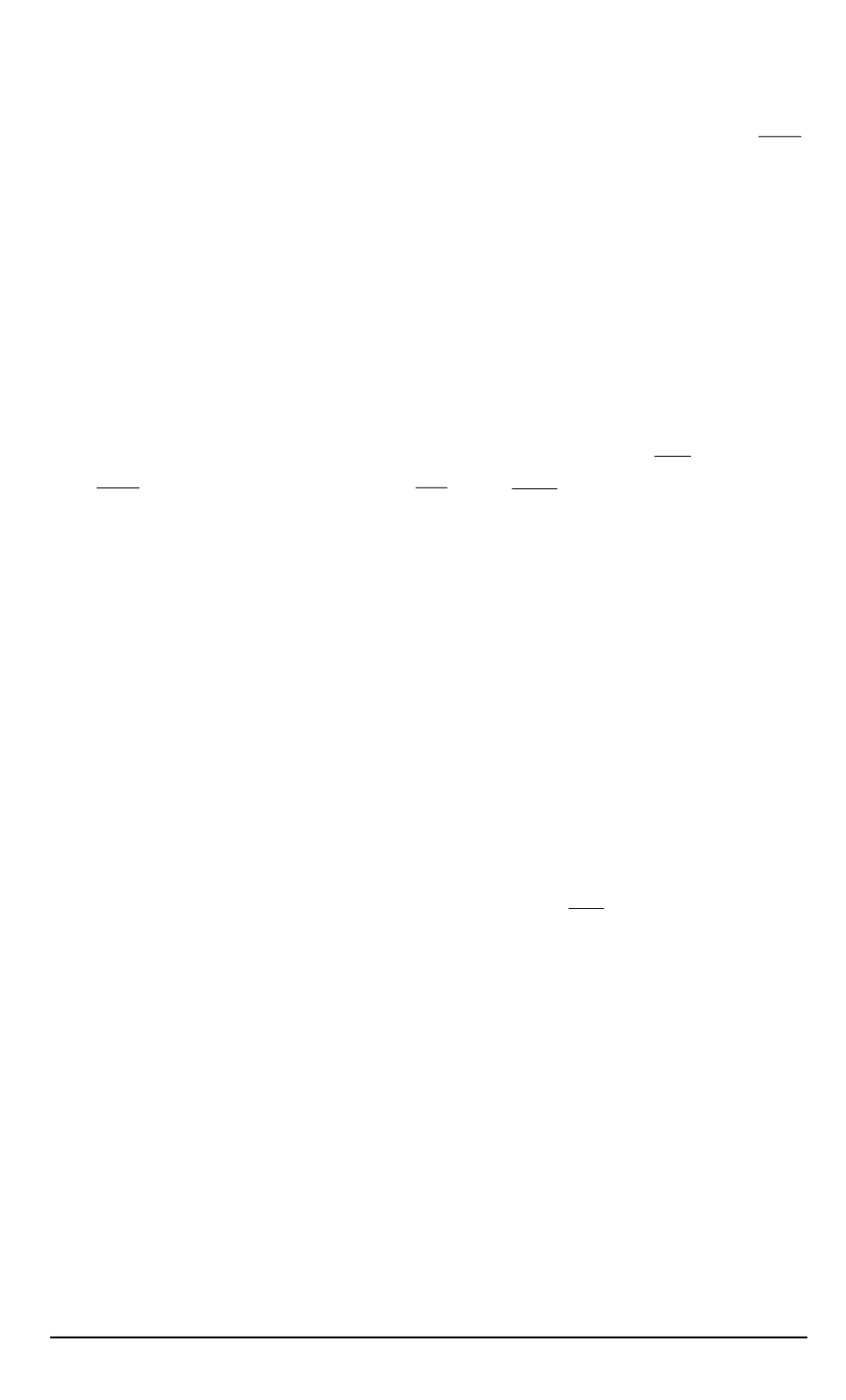
но и когда не будет обслужено ни одной заявки
,
и новая поступающая
в систему заявка будет потеряна
.
Таким образом
,
матрица
P
переходных вероятностей вложенной це
-
пи Маркова
,
представленная в блочной форме
P
= (
P
kn
)
, k, n
= 1
, R
,
имеет следующий вид
:
P
=
A
∗
1
A
0
0
. . .
0
0
A
∗
2
A
1
A
0
. . .
0
0
A
∗
3
A
2
A
1
. . .
0
0
. . . . . . . . . . . . . . . . . . . . . . . . .
A
∗
r
A
r
−
1
A
r
−
2
. . . A
1
A
0
A
∗
R
A
r
A
r
−
1
. . . A
2
A
1
+
A
0
.
Можно показать
,
что вложенная цепь Маркова является неприво
-
димой и непериодической
.
Обозначим через
p
∗
ik
, i
= 1
, d, d
=
ml
,
k
= 1
, R
,
где
i
=
l
(
n
−
1) +
j, j
= 1
, l, n
= 1
, m
,
стационарную по вло
-
женной цепиМаркова вероятность того
,
что в системе имеется
k
заявок
,
фаза
,
на которой находится процесс поступления заявок
,
n
-
я и фаза об
-
служивания
j
-
я
,
и положим
~p
∗
k
= (
p
∗
1
k
, . . . , p
∗
dk
)
т
,
~p
∗
= (
~p
∗
1
т
5
, . . . , ~p
∗
R
т
)
т
.
Тогда для
~p
∗
справедлива система уравнений равновесия
(
СУР
)
~p
∗
т
=
~p
∗
т
P,
(3)
или
,
в координатной форме
,
~p
∗
1
т
=
R
X
m
=1
~p
∗
m
т
A
∗
m
,
(4)
~p
∗
k
т
=
R
X
m
=
k
−
1
~p
∗
m
т
A
m
−
k
+1
, k
= 2
, r,
(5)
~p
∗
R
т
=
~p
∗
r
т
A
0
+
~p
∗
R
т
(
A
0
+
A
1
)
(6)
с условием нормировки
p
∗
·
,
·
= 1;
(7)
здесь символ
“
·
”
означает суммирование по всем значениям соответ
-
ствующего дискретного аргумента
.
СУР
(3)
имеет единственное
,
с условием нормировки
,
решение
,
ко
-
торое можно получить методом
,
приведенным в рабое
[2].
Зная стационарное распределение вложенной цепи Маркова
,
не
-
трудно определить другие стационарные характеристики обслужива
-
ния в рассматриваемой системе
.
64
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2004.
№
2