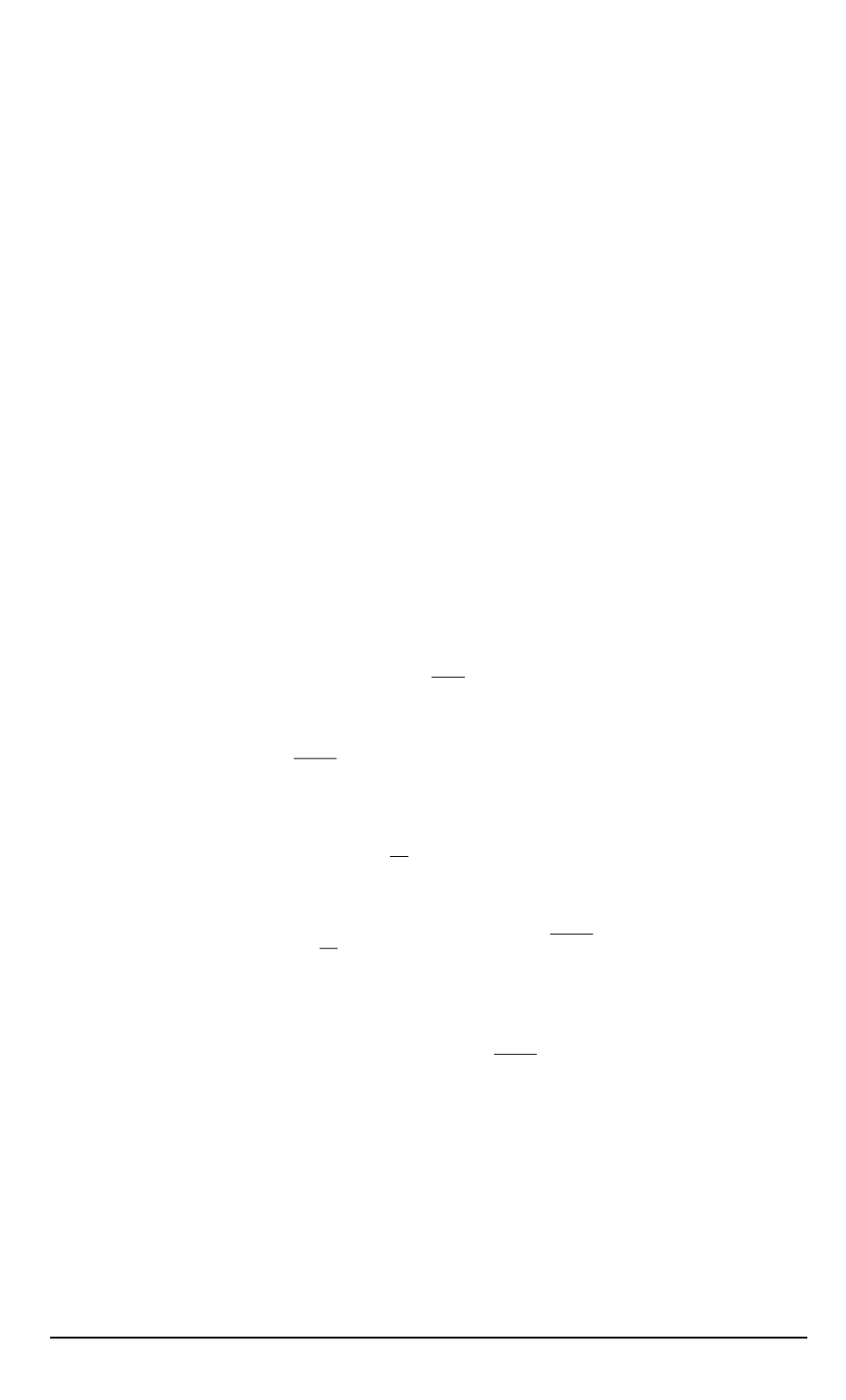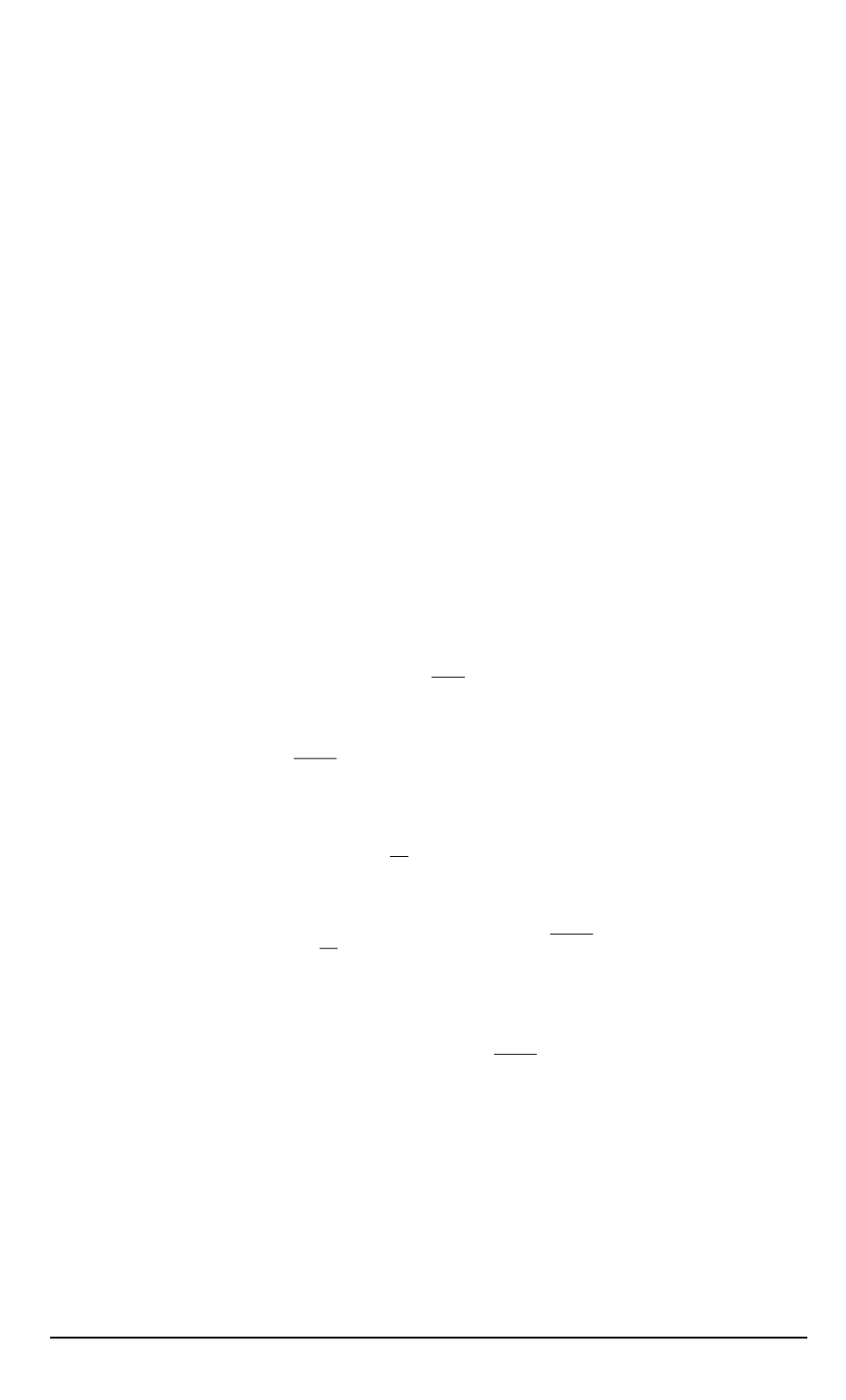
где
~b
—
вектор с координатами
b
i
=
∞
R
0
t dB
i
(
t
)
.
Среднее время
T
между соседними моментами изменения состоя
-
ний вложенной цепи Маркова в стационарном режиме функциониро
-
вания системы определяется формулой
T
=
R
X
k
=0
~p
∗
k
т
~t
=
R
X
k
=0
~p
∗
k
т
(
~b
⊗
~
1
l
)
.
(8)
Рассмотрим соотношение
T
= (
~π
a
)
т
M
ij
b
ij
~
1
m
.
Действительно
,
(
~π
a
)
т
=
~p
∗
k
т
L
,
где
L
=
I
m
⊗
~
1
l
и
~b
=
M
(
b
ij
)
~
1
m
.
Перемно
-
жая матрицу
L
и вектор
~b
,
получаем
L~b
=
~b
⊗
~
1
l
,
откуда немедленно приходим к формуле
(8).
Заметим также
,
что загрузку системы
ρ
можно представить в виде
ρ
=
1
Tµ
.
Используя результаты теории полумарковских процессов
,
получаем
для векторов
~p
k
, k
= 0
, R
,
стационарных вероятностей состояний по
времени формулы
~p
т
0
=
1
T
R
X
m
=1
~p
∗
m
т
T
∗
m
,
~p
т
k
=
1
T
R
X
m
=
k
~p
∗
m
т
T
m
−
k
, k
= 1
, R.
Введем обозначение
~q
k
=
~p
k
т
Q, k
= 0
, R,
где
Q
= 1
m
⊗
I
l
.
Получим соотношение между векторами
~q
k
и
~π
s
,
которое будем ис
-
пользовать в дальнейшем
.
Для этого заметим
,
что матричные функции
F
k
(
x
)
удовлетворяют дифференциальному уравнению
F
0
k
(
x
) =
F
k
(
x
)Λ +
u
(
k
)
F
k
−
1
(
x
)
N, k
≥
0;
66
Вестник МГТУ им
.
Н
.
Э
.
Баумана
.
Сер
. "
Естественные науки
". 2004.
№
2