Система массового обслуживания SM/MSP/l/r1 - page 9

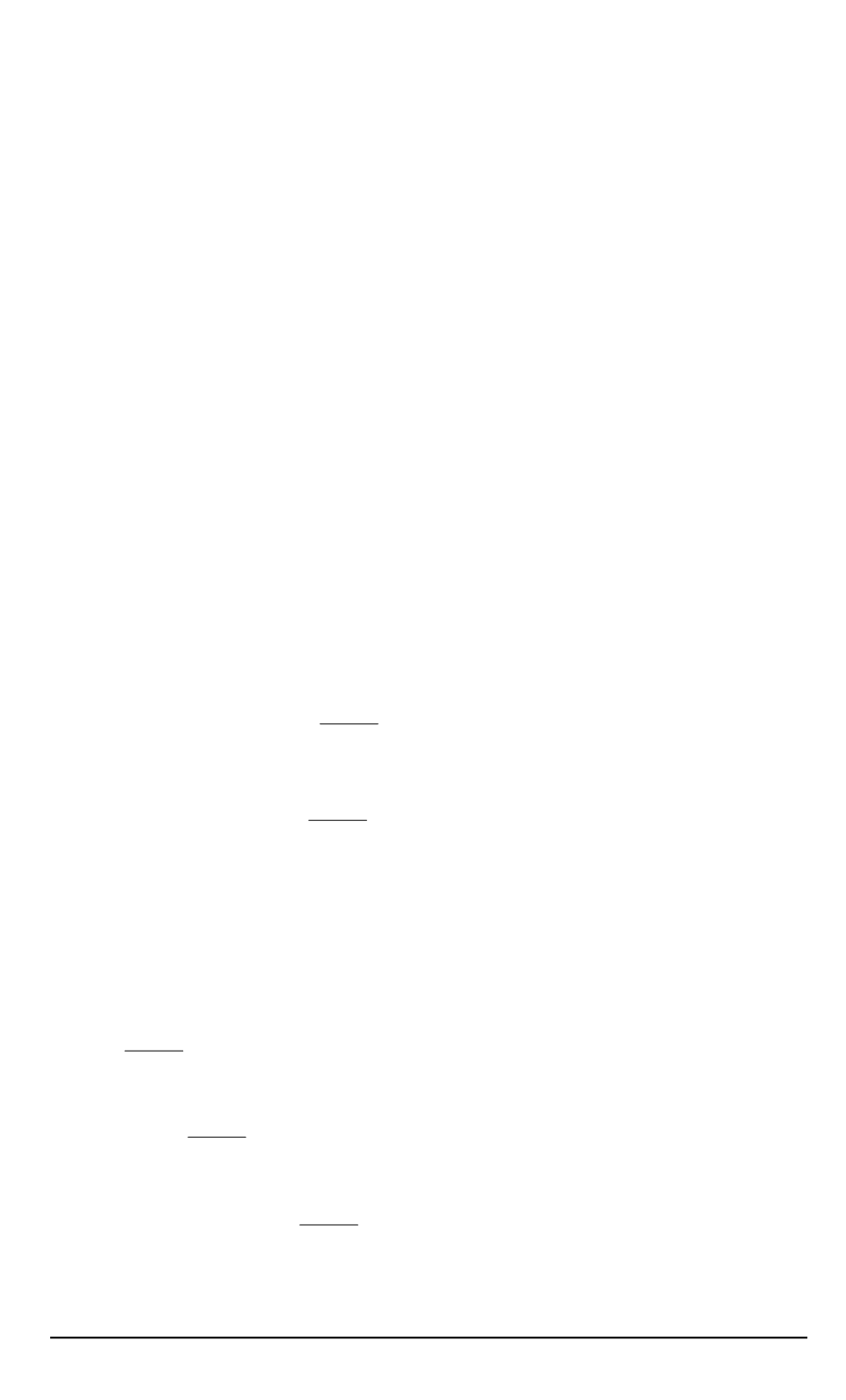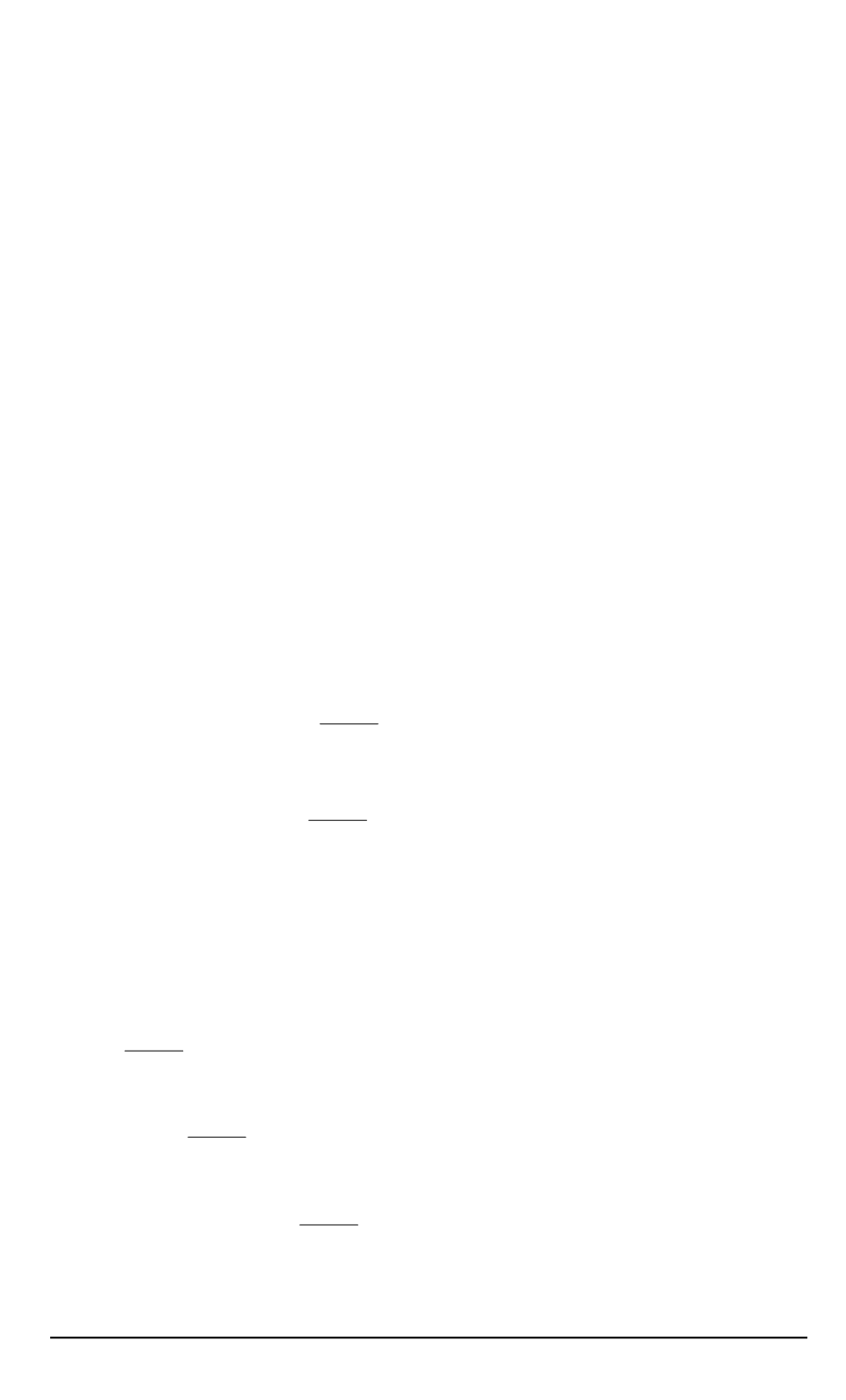
обслужено не менее k заявок и в момент окончания обслуживания k-й
заявки процесс обслуживания перейдет на j- ю фазу при условии, что в
начальный момент фаза обслуживания была i-я и в системе находилось
не менее k заявок, а через Φ k (s ) обозначим преобразование Лапласа –
Стилтьеса матрицы Vk ( x). Обозначим также через fk ( s) , k ≥ 0, пре-
образование Лапласа–Стилтьеса матрицы Fk ( s) , которая введена ранее.
Поскольку вероятность того, что обслуживание группы из m заявок,
m < k, окончится на временн´ ом интервале [x, x + dx) при условии, что
до этого момента уже обслужено k − m заявок, определяется формулой
Fk −m Λ∗
m dx, и поскольку за время x может быть обслужено от 1 до k − 1
заявок, имеем
Φ 1 (s ) =
∞ Z0
e− sxeΛx Ndx = (sI − Λ)− 1N,
Φ k (s ) = Φk
1 (s ), k ≥ 2.
Отсюда нетрудно получить преобразования Лапласа–Стилтьеса
ω( s) и ϕ( s) стационарных распределений W ( x) и V ( x) — времени
ожидания начала обслуживания и времени пребывания в системе про-
извольной заявки, принятой к обслуживанию:
ω( s) =
1
1 − π
r Xk=0
~p −
k
т( Im ⊗ Φk ( s))~1,
ϕ( s) =
1
1 − π
r Xk =0
~p −
k
т(I m ⊗ Φ k+1 (s ))~1.
Дифференцируя эти формулы в точке s = 0, получаем для среднего
времени w ожидания начала обслуживания и среднего времени v пре-
бывания в системе произвольной заявки, принятой к обслуживанию,
для стационарного режима функционирования системы выражения
w = − 1
1 − π
r Xk=1
~p −
k
т( Im ⊗ Φ0
k (0))~1 =
= − 1
1 − π
r Xk=1
~p −
k
т Ã Im ⊗ Ã k −1 Xj =0
( −Λ− 1 N ) j Λ− 1 !! ~1 =
= −
1
1 − π
r− 1 Xj =0
r X
k = j+1
~p −
k
т ¡ Im ⊗ ¡( −Λ− 1N ) j Λ− 1¢¢ ~1,
68 Вестник МГТУ им. Н.Э. Баумана. Сер. " Естественные науки". 2004. № 2