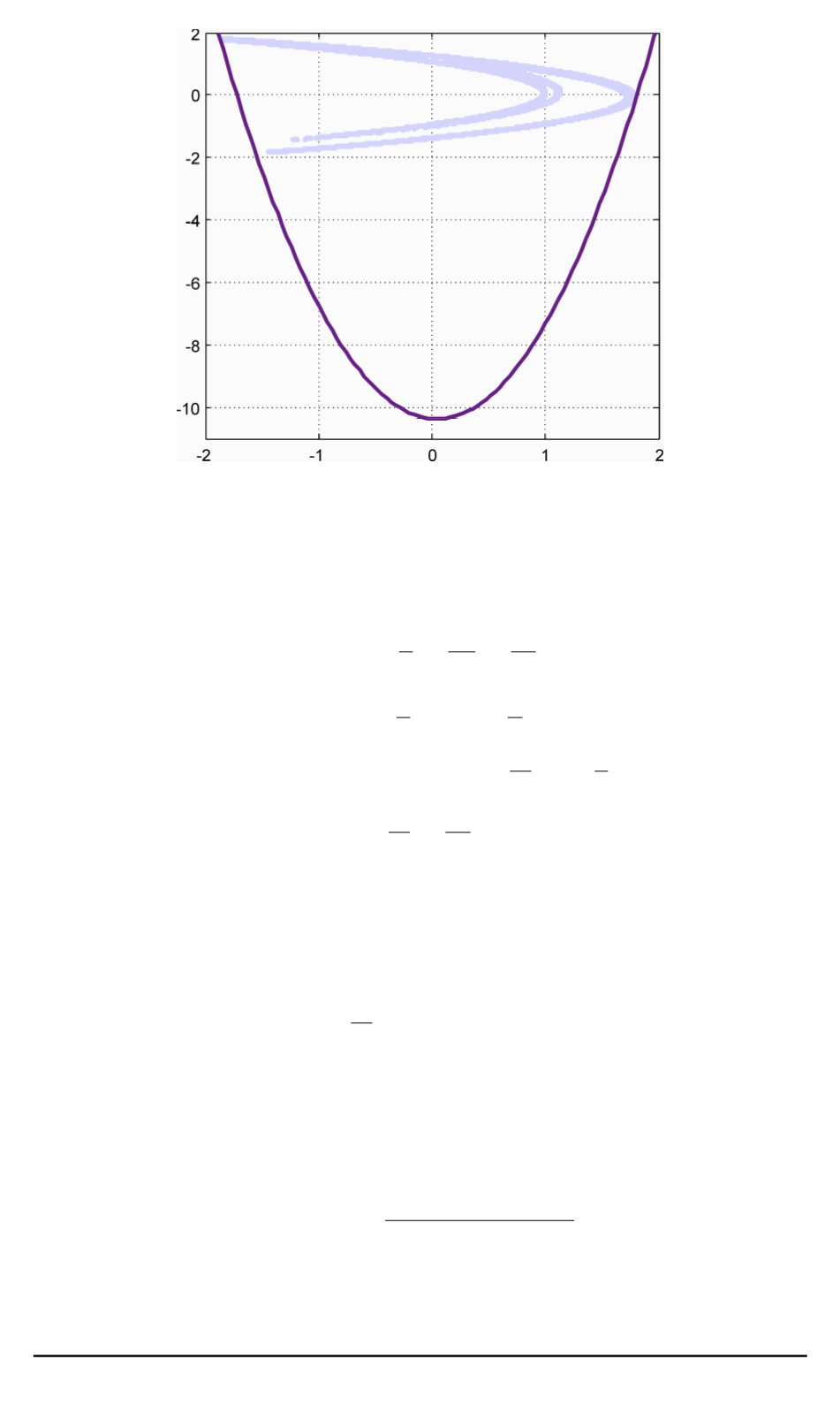
Рис. 1. Траектория системы Хенона и граница локализирующего множества
для робастно положительно инвариантных компактов
системе (6) является система
x
n
+1
=
y
n
,
y
n
+1
=
−
a
b
+
x
n
b
+
y
2
n
b
.
(16)
Заменой переменных
ξ
=
−
y
b
,
η
=
−
x
b
система (16) сводится к
самой системе Хенона с параметрами
˜
a
=
a
b
2
,
˜
b
=
1
b
:
ξ
n
+1
=
a
b
2
+
η
n
b
−
ξ
2
n
,
η
n
+1
=
ξ
n
.
(17)
Поэтому локализирующие множества для положительно инвариант-
ных компактов системы (16) можно получить, исходя из результатов
построения локализирующих множеств для системы Хенона. Пара-
метр неопределенности
˜
a
=
a
b
2
меняется на отрезке
[
a /b
2
, a /b
2
]
. По-
ложив
˜
a
=
a /b
2
,
˜
a
=
a /b
2
, из неравенства (12), описывающего се-
мейство локализирующих множеств для положительно инвариантных
компактов системы Хенона, путем замены переменных и параметров
получим
−
ξ
−
λη
≤
4
λ
2
˜
a
+ (
λ
2
−
˜
b
)
2
4
λ
( ˜
b
−
λ
)
,
откуда, восстанавливая исходные переменные и параметры, находим
неравенство, описывающее семейство локализирующих множеств для
16
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2011. № 3


