множество для положительно инвариантных компактов обратной си-
стемы и переходя к исходным переменным и параметрам, получаем
семейство локализирующих множеств
λx
+
y
≤
4
λ
2
a
∗
+ (
λ
2
b
−
1)
2
4
λ
(1
−
bλ
)
, λ
∈
0
,
1
b
.
Пересечение этого семейства описывается неравенством
y
≤
1
b
min
μ
∈
(0
,
1)
−
μx
+
4
μ
2
a
∗
+ (
μ
2
−
b
)
2
4
μ
(1
−
μ
)
.
Используя семейство (13) локализирующих множеств для положи-
тельно инвариантных компактов, вычисленное для обратной системы,
в результате перехода к исходным переменным и параметрам получа-
ем семейство локализирующих множеств для отрицательно инвари-
антных компактов системы (5):
y
2
+
μy
+
x
≤
a
∗
+
4
μ
2
a
∗
+ (
μ
2
−
b
)
2
4
μ
(1
−
μ
)
.
Пересечение этого семейства описывается неравенством
x
≤
a
∗
−
y
2
+ min
μ
∈
(0
,
1)
−
μy
+
4
μ
2
a
∗
+ (
μ
2
−
b
)
2
4
μ
(1
−
μ
)
.
(16)
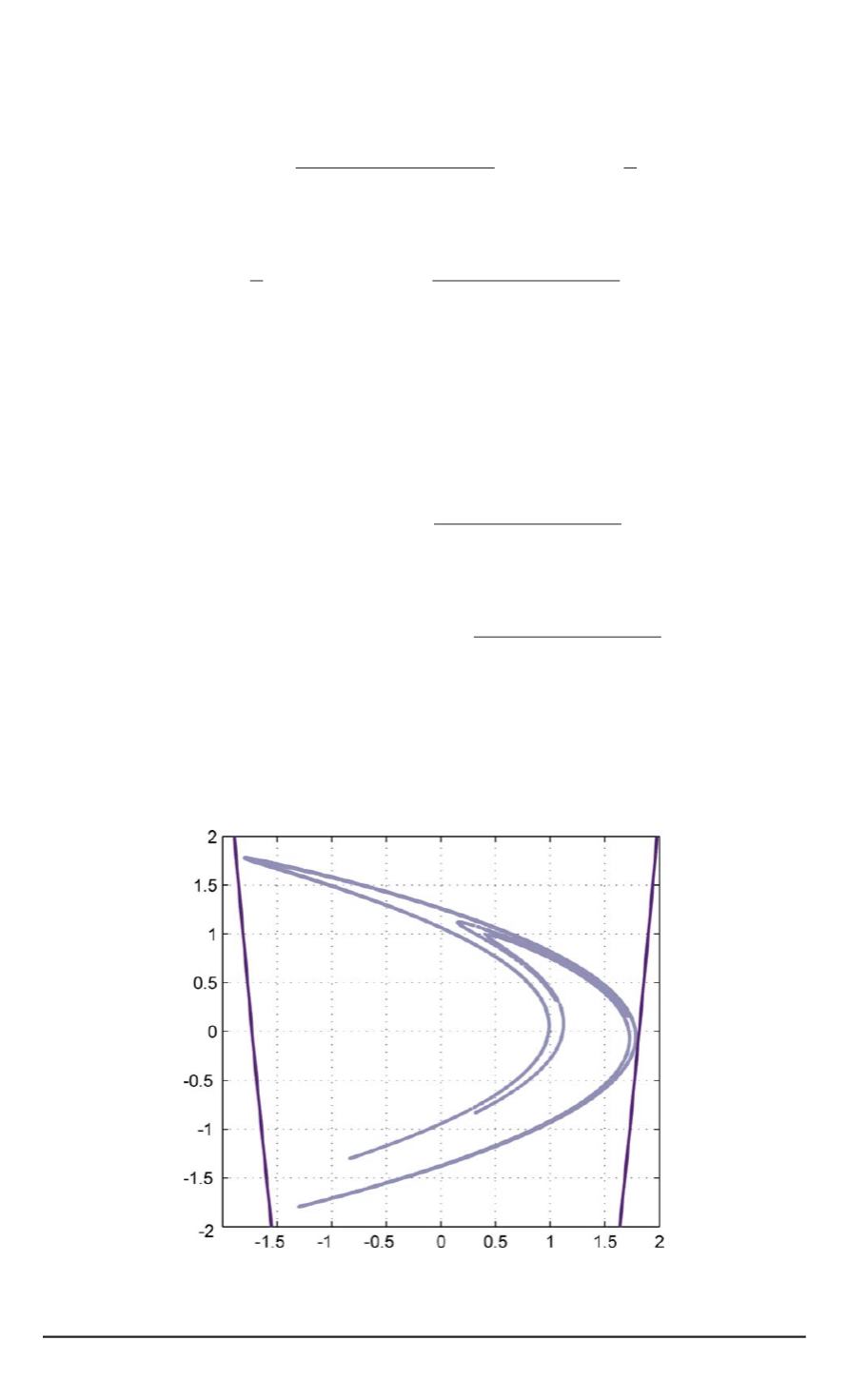
На рис. 2 изображены траектория системы Хенона (5) с параме-
трами
a
∗
= 1
,
38
,
a
∗
= 1
,
42
,
b
= 0
,
3
и граница локализирующего
множества (16). Траектория построена при чередующемся управле-
нии:
u
n
= 1
,
38
при нечетном
n
и
u
n
= 1
,
42
при четном
n
.
Рис. 1. Траектория управляемой системы Хенона и локализирующее множество
(14) для положительно инвариантных компактов
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. “Естественные науки”. 2012. № 1
15


