
Предельные теоремы для случайного блуждания в полуплоскости с перескоком границы
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2016. № 6
17
Для случайного блуждания
0
( , )
n n
S S
возможна остановка в одном из состояний
множества
0
0
{( , ),
,
= 0, ,
1}.
Z
k
Вероятности остановки равны
0
0
0
0
( , )
( , )
( , )
( , )
=
( ),
lim
n
q
P n
а при = 1
k
есть вероятности достижения границы
полуплоскости
0
0
{( ,
1),
},
k
Z
при = 0, ,
2
k
— вероятности перескока
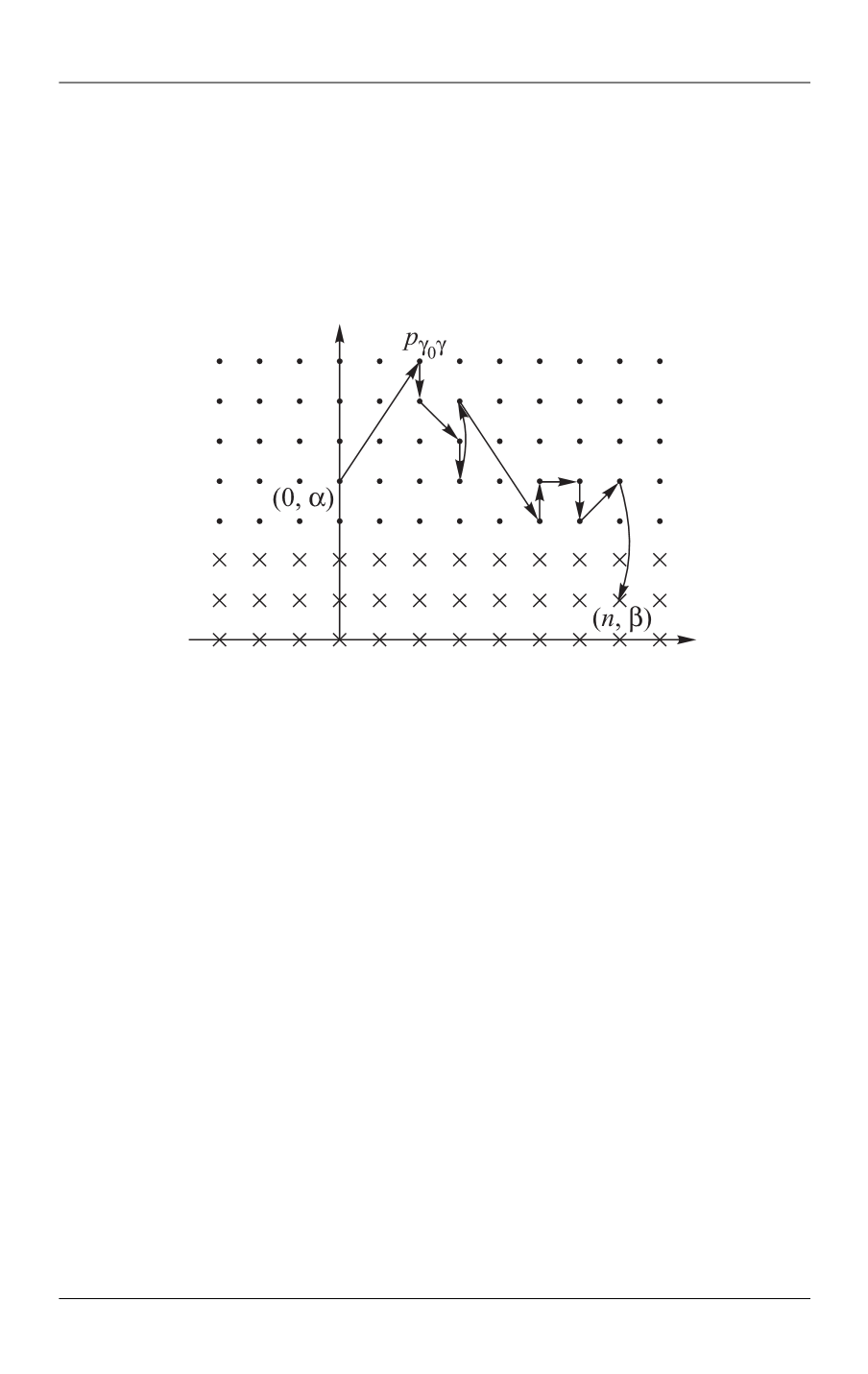
этой границы. Одна из реализаций случайного блуждания
0
( , )
n n
S S
при началь-
ном состоянии
(0, )
и остановкой в состоянии ( , )
n
показана на рисунке.
Реализация случайного блуждания
( = 3),
k
точки остановки
обозначены знаком «
»
Введем производящую функцию вероятностей скачков,
| | 1,
u
| | 1,
s
0
0
0
, =0
( , ) =
.
h u s
p u s
(1)
Явные выражения для вероятностей остановки при общих предположениях
о производящей функции
( , )
h u s
получены в работе [2]. Настоящая работа явля-
ется продолжением указанной работы. Установлены предельные теоремы для
точки выхода случайного блуждания на границу полуплоскости и для точки пе-
рескока этой границы в докритическом, критическом и надкритическом случа-
ях. Обобщен случай
=1
k
[3, 4], когда перескока через границу полуплоскости
нет. Теоремы 2–5 приведены в краткой заметке [5].
Выражение для вероятностей остановки
(0, )
( , )
n
q
[2].
Учитывая равенство
0
0
( , )
(0, )
( , )
(
, )
=
,
n
n
q
q
далее рассмотрим вероятности
(0, )
( , )
.
n
q
Введем производящие
функции,
| | 1,
u
(0, )
( , )
=0
( ) =
,
,
= 0, ,
1.
n
n
n
u q u
N
k
(2)
















