
Численная схема высокого порядка точности…
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2016. № 6
99
вихревого слоя на каждой панели, сделав соответствующее распределение ку-
сочно-линейным или кусочно-квадратичным.
Учет каждого фактора в отдельности позволяет обеспечить лишь незначи-
тельное повышение точности и не повышает порядок точности схемы.
Известно [1], что интенсивность вихревого слоя неограниченно возрастает
вблизи «внешних» угловых точек профиля (т. е. в тех случаях, когда угол между
касательными к сторонам угла больше развернутого, если смотреть со стороны
потока), поэтому гладкие части профиля при построении схем повышенного
порядка точности с необходимостью следует аппроксимировать гладкими кри-
выми. Будем предполагать, что форма профиля известна точно и она описыва-
ется кусочно-гладкими параметрическими зависимостями
= ( ),
x x t
= ( ),
y y t
[0, 2 ).
t
Таким образом, можно считать, что известны не только координаты
отдельных точек на профиле, определяющих концы панелей, но и направления
касательных к профилю в этих точках.
Потребуем, чтобы кривая, аппроксимирующая профиль, проходила через
заданные точки, а также имела в этих точках то же направление касательной,
что и исходный профиль.
Обозначим начало и конец
i
-й панели через
i
C
и
1
i
C
(эти точки соответ-
ствуют значениям параметра =
i
t t
и
1
=
i
t t
в параметрических уравнениях
профиля); пусть
0
i
— единичный вектор, сонаправленный с вектором
1
;
i i
C C
0
i
n
— единичный вектор, ортогональный вектору
0
i
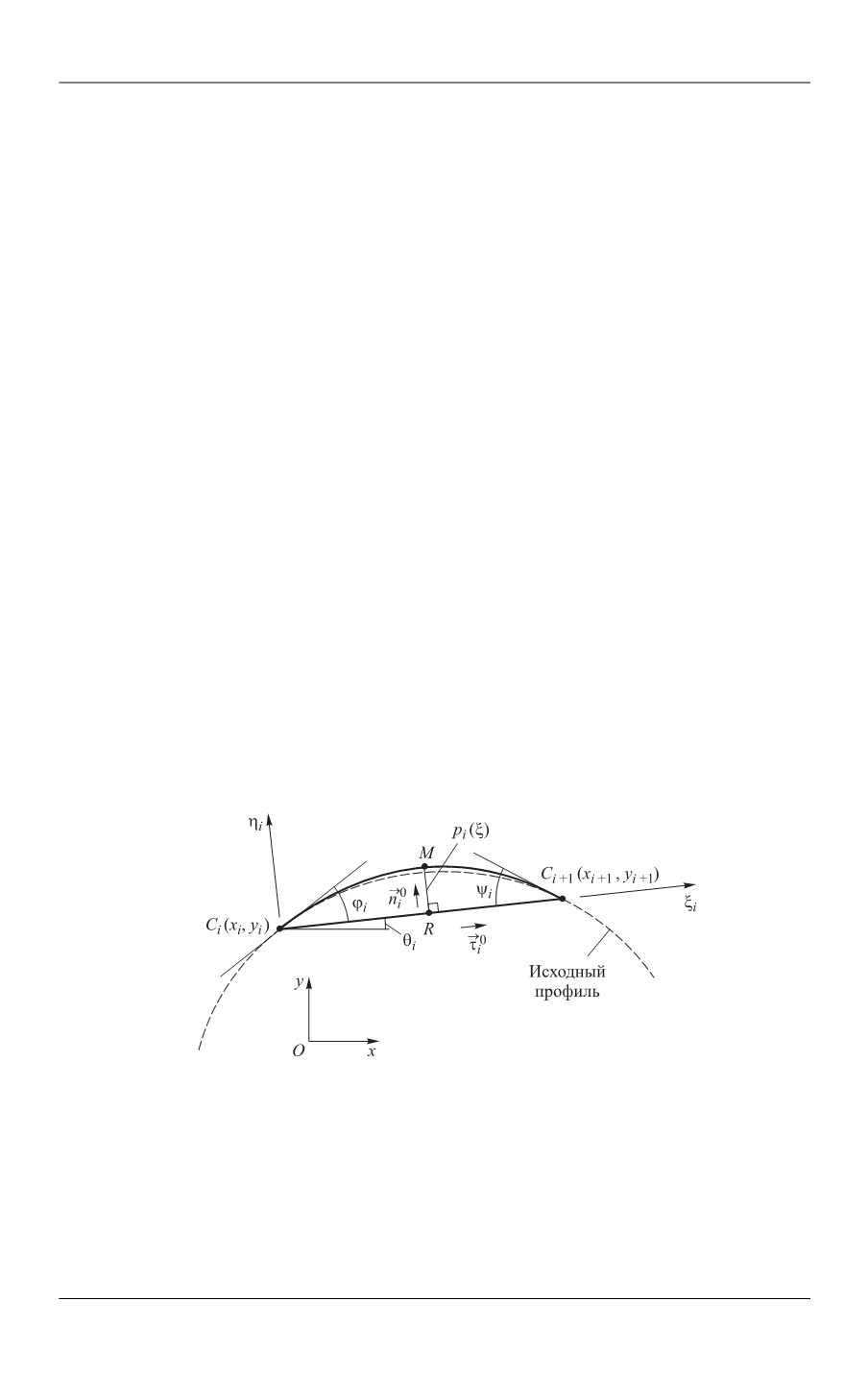
(рис. 2). Под «панелью
профиля» теперь будем понимать прямолинейный отрезок, соединяющий точ-
ки
i
C
и
1
;
i
C
при этом в общем случае участки профиля имеют с соответствую-
щими панелями лишь общие концы.
Рис. 2.
Кусочно-полиномиальная аппроксимация профиля
На каждой панели введем локальную систему координат
,
i i i
C
тогда точ-
ки
i
C
и
1
i
C
имеют локальные координаты
(0, 0)
и
( , 0),
i
L
где
1
=|
|.
i
i i
L C C
Для
построения интерполяционной кривой сначала вычислим тангенсы углов
наклона касательной к панели
i
и
i
(см. рис. 2), используя следующие соот-
ношения:
















