
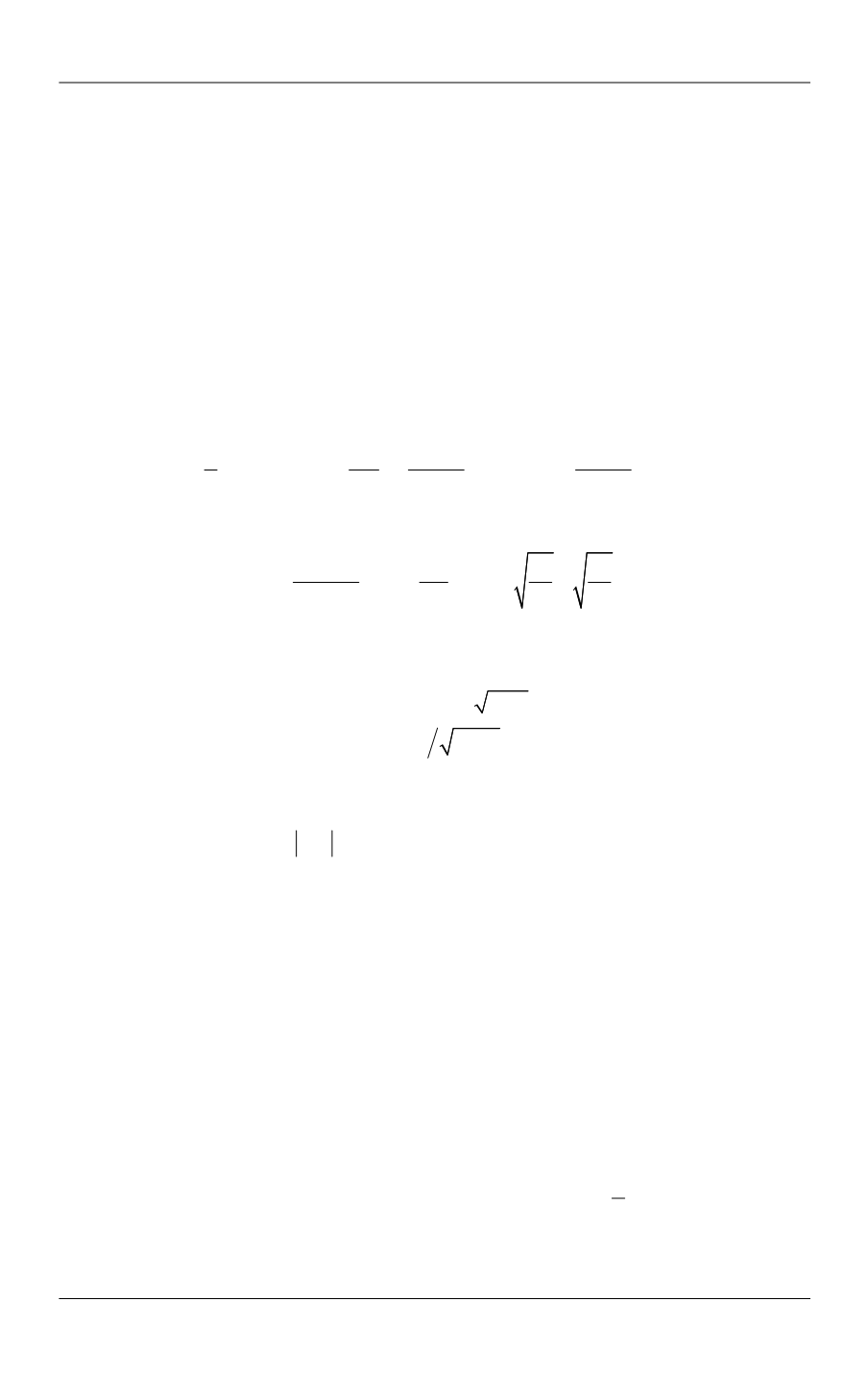
Взаимодействие уединенных волн в двухжидкостной магнитной гидродинамике…
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 1
63
относятся к волновым пакетам и являются частными решениями системы (8)
для
0.
q
Численное исследование их столкновений представлено ниже. Слу-
чай
0
q
соответствует инвариантности системы (8) относительно вращений в
поперечной плоскости.
Решение уравнений бегущих волн (8) в случае
q 0.
Система (8) в случае
0
q
полностью интегрируется. Оказывается, что удачной заменой независи-
мой переменной ее можно свести к динамической системе, описывающей дви-
жение материальной точки в поперечной плоскости в специальном поле сил и
тогда полная интегрируемость системы (8) следует из общих теорем классиче-
ской механики. Однако рассмотрим более простой путь. Перепишем систему (8)
для
0
q
в безразмерном виде
2
2
2
2;
,
0,
2
u H
d d
d
u b
u u
bu
d
d
d
H
H
H
k
(10)
где
, ,
b
— безразмерные параметры, равные
2
2
2
0
0
0
,
,
.
4
i e
i
e
e
i
H
c
b
L
H
Здесь
0 0 0 0
,
,
,
L H V
— характерные масштабы длины, напряженности магнит-
ного поля, скорости и плотности, при этом выбор параметров
0 0 0
,
,
H V
увязан
с константами бегущей волны
J
и
D
−
0
4 ,
H D
2
0
4 / ,
J D
0
/(2 ).
V D J
То-
гда, как нетрудно проверить,
0
0
0
4 .
V H
Параметр
0
/(
)
p
c
L
равен
отношению скиновой длины
/
p
c
к характерному линейному масштабу, где
p
— плазменная частота. Таким образом, решение системы (10) находится в
фиксированной области
2
H
и зависит от параметров
, .
b
Для решения системы (10) примем
(0,
,
)
y z
H H
H
и перейдем в попереч-
ной плоскости к полярным координатам
cos ,
sin .
y
z
H H H H
Итак, вме-
сто функций
( ),
( ),
y
z
H H
удовлетворяющих системе (10), будем искать функ-
ции
( ), ( ),
H
удовлетворяющие системе дифференциальных уравнений, ко-
торая получится при подстановке величин
( ), ( )
H
в систему (10). Далее
производные по
также обозначены точкой над функцией. В результате полу-
чают систему уравнений
cos
sin 0;
cos
sin 0,
A B
B
A
(11)
где
2 2
2
2
2
2
2 2
2 2
( ) 2 ( )
;
2
2
2
.
u
A u H H
uH H buH b H
B u H H uH H buH
















