
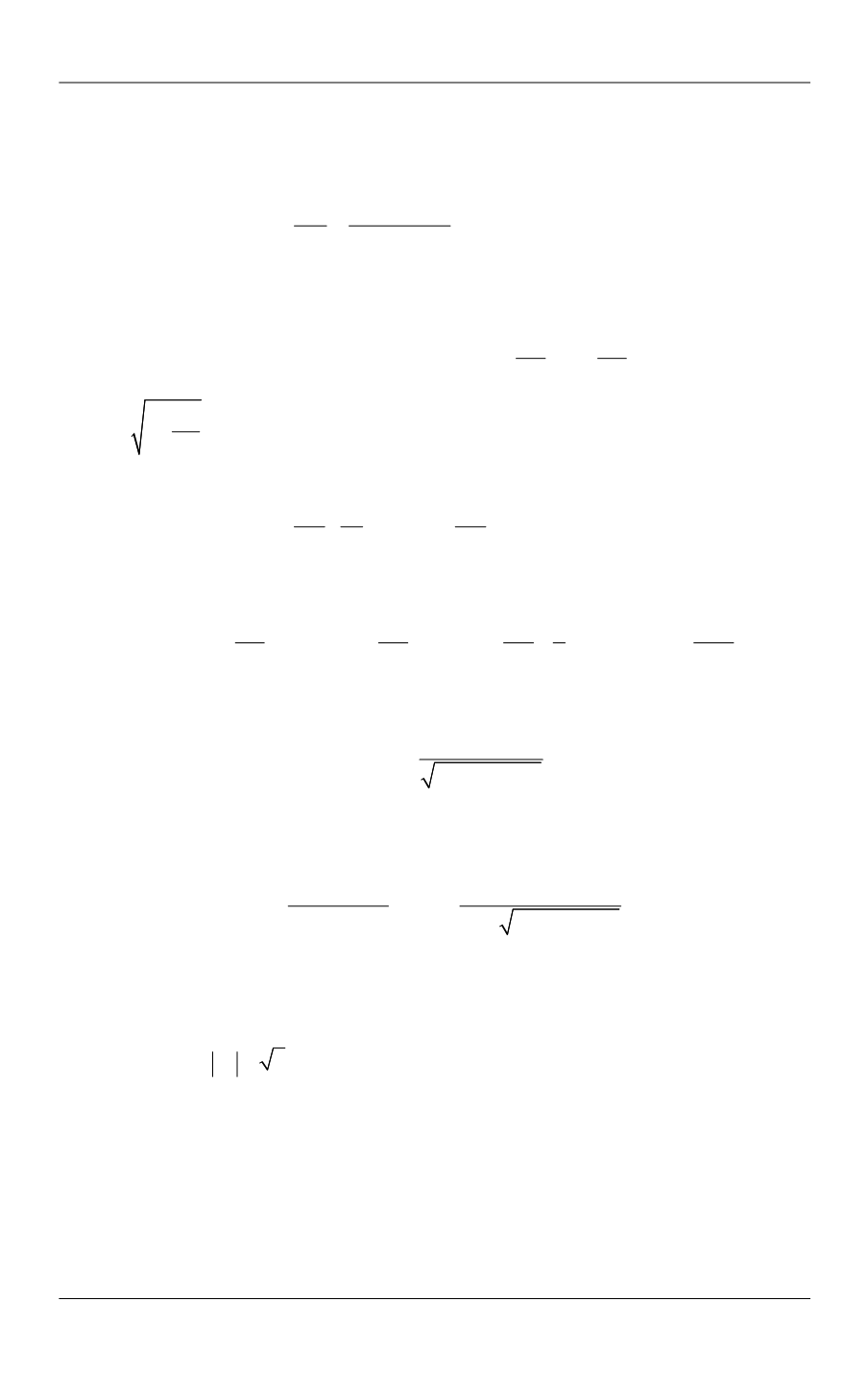
М.Б. Гавриков, В.В. Савельев
64
ISSN 1812-3368. Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2017. № 1
Соотношения (11), очевидно, равносильны равенствам
0,
0,
A B
которые и
образуют искомую систему для нахождения функций
( ), ( ).
H
Условие
0
B
может быть проинтегрировано. Тогда запишем
2
2
2
,
const.
2
d
bH
d
u H
(12)
Подставляя (12) в равенство
0,
A
получаем уравнение для нахождения функции
( ) :
H
2
2
2 2
2
2
2 2
3
2 ( )
1
0,
2
H
u H uH H
b
H
H
(13)
где
2
2
1 ;
2 .
4
u H
Уравнение (13) легко интегрируется. Умножая (13) на
,
H
определяем
2
2
( )
( ) 0.
2
d
d
uH
H
d
d
Здесь
( )
H
— потенциальная функция,
2
2
4
2
2 2
2 2 2
3
2
1
( )
1
(1
)
.
2
8 2
2
H
H
H
b
H dH
b H
H
H
(14)
Откуда
2
(2 )
( )
,
2(
( ))
H dH
H
E H
(15)
где
E
— произвольная константа. Теперь из (12) с учетом (15) находим функ-
цию
2
2
2
2
2
2
( )
.
2
2 2(
( ))
bH
bH
H
d
dH
u H
H E H
(16)
Причем знаки в (15) и (16) соответствуют друг другу. Формулы (15), (16) поз-
воляют определить функции
( ), ( ),
H H
а также
( ), ( ).
H
Согласно приведен-
ным формулам, решение расположено в «потенциальных ямах»
( ) ,
H E
лежа-
щих в области
2,
H
и на всей прямой
«склеивается» из «дуг»,
задаваемых формулами (15), (16). Несложно показать, что за исключением вырож-
денных случаев эти «дуги» выражаются через эллиптические интегралы. Анализ
возникающих при этом случаев зависит от вида потенциальной функции
( )
H
и
приведен в работе [7]. Здесь интересны только решения типа уединенной волны,
которые относятся к вырожденным случаям и возникают только тогда, когда пря-
мая
const
E
касается одного (и только одного) края потенциальной ямы
( ) .
H E
Такая ситуация возникает только при
0
и
2 2
1.
b
Тогда потенци-
















